Estadística
(Página creada con «<span style="font-size:200%;;color: #e2007a">Estadística</span> <div style="float:right">__TOC__</div> {{#TwitterFBLike:left|like}} 600px...») |
|||
| Línea 61: | Línea 61: | ||
[[Archivo:3 ESTADISTICA gráfica1.png |400px]] | [[Archivo:3 ESTADISTICA gráfica1.png |400px]] | ||
| − | |||
| − | |||
¿Qué mes tuvo un mayor promedio de asistencia? | ¿Qué mes tuvo un mayor promedio de asistencia? | ||
| Línea 72: | Línea 70: | ||
d. Junio | d. Junio | ||
| − | |||
| − | |||
| − | |||
|} | |} | ||
{| style="background:LavenderBlush" border="1" cellpadding="5" cellspacing="0" align="center" | {| style="background:LavenderBlush" border="1" cellpadding="5" cellspacing="0" align="center" | ||
| Línea 80: | Línea 75: | ||
|+ align="center" style="background:#e2007a; color:white"|<big>'''Descripción del ítem'''</big> | |+ align="center" style="background:#e2007a; color:white"|<big>'''Descripción del ítem'''</big> | ||
| − | | colspan=2|'''Competencia básica 3: | + | | colspan=2|'''Competencia básica 3: Pensamiento lógico-matemático''' |
|- | |- | ||
| − | |'''Dimensión clave'''|| | + | |'''Dimensión clave'''||Conocimiento y manejo de los elementos matemáticos básicos. |
|- | |- | ||
| − | |'''Componente'''|| | + | |'''Componente'''||Integración y aplicación de conocimientos estadísticos. |
|- | |- | ||
| − | |'''Indicador de logro'''|| | + | |'''Indicador de logro'''||Explica la información que presentan diferentes tipos de gráficas. |
|- | |- | ||
| − | |'''Contenido evaluado'''|| | + | |'''Contenido evaluado'''||Uso de gráfico de barras |
|- | |- | ||
| − | |'''Demanda cognitiva'''|| | + | |'''Demanda cognitiva'''||Comprensión |
|- | |- | ||
|style="background:Grey; color:white"|'''Respuesta correcta'''||style="background:Grey; color:white"|<u>Opción b</u> | |style="background:Grey; color:white"|'''Respuesta correcta'''||style="background:Grey; color:white"|<u>Opción b</u> | ||
|} | |} | ||
| + | == <span style="color: #e2007a;">Análisis del error</span> == | ||
| + | {| style="background-color:#ececed; float:left" width="20%" | ||
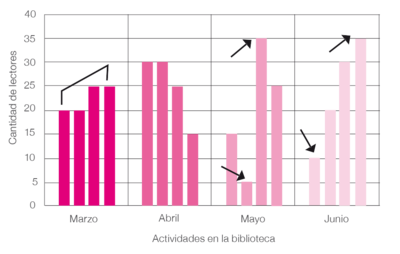
| + | |El ítem presenta una gráfica de barras, el estudiante debe identificar cuál de los meses que se muestran obtuvo un mayor promedio basándose en el análisis | ||
| + | de frecuencias. | ||
| + | [[Archivo:3 ESTADISTICA gráfica3.png|400px]] | ||
| + | Los estudiantes no fueron capaces de comprender la información en la gráfica de barras, no identificaron la escala de la cantidad de lectores como indicador | ||
| + | de la frecuencia de lectores en los distintos meses y/o no fueron capaces de incorporar el concepto de promedio a través de la visualización de los datos. | ||
| + | |} | ||
| + | Si seleccionaron la opción '''a''', los estudiantes no identificaron que marzo fue uno de los meses en que el promedio de asistencia fue menor. Omitieron información de la gráfica como un rango pequeño, valores similares y un valor máximo (25) menor a los valores máximos observados en otros meses. | ||
| + | |||
| + | Quienes eligieron la opción '''c''' o la opción '''d''' probablemente observaron el valor máximo de lectores que asistieron a las actividades de la biblioteca esos meses (35), pero no reconocieron que el promedio se ve afectado por valores mínimos y máximos extremos, como se observa en las barras de mayo y junio; ambos meses tienen un rango amplio de frecuencia. | ||
| + | |||
| + | Si los estudiantes no dominan conceptos de medidas de tendencia central, no podrán interpretar de manera adecuada gráficos que las ilustran. No necesitan calcular el promedio de cada mes; con identificar que la gráfica ilustra igual cantidad de actividades en cada mes, podrían calcular la frecuencia total de lectores que asiste mensualmente y con ello inferir el mes con una media mayor. Esto no resulta posible si hay una debilidad en la comprensión del concepto y cálculo de un promedio de datos. | ||
| + | |||
| + | [[Archivo:3 ESTADISTICA gráfica4.png|400px]] | ||
| + | |||
| + | |||
| + | == <span style="color: #e2007a;">Sugerencias de estrategias de enseñanza-aprendizaje</span> == | ||
| + | {| style="background:#e2007a;border:1px solid #e2007a;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| + | | | ||
| + | <span style="color: #ffffff;"> | ||
| + | La comprensión de los gráficos es la habilidad que permite a los estudiantes obtener información a partir de un gráfico creado por ellos mismos o por otros. Esta comprensión puede darse en tres niveles que deben procurarse en la enseñanza de la estadística: racional/literal –leer los datos–, crítico –leer entre datos– e hipotético –leer más allá de los datos– (Espinel et. al, 2009). | ||
| + | |} | ||
| + | |||
| + | 1. Buscar en periódicos y medios de comunicación gráficos de barras, utilizarlos para identificar elementos gráficos, para analizar la claridad de la información presentada, el contexto de los datos, el objetivo del gráfico en la comunicación. | ||
| + | |||
| + | 2. Favorecer el uso de información disponible sobre la comunidad. Pueden ser datos sobre encuestas nacionales, datos de salud, indicadores educativos, | ||
| + | indicadores municipales, etc. Contar con datos reales del contexto propio favorecerá el significado que se dé a los aprendizajes. Los estudiantes pueden | ||
| + | identificar en esta información, qué tipo de variables se presentan como datos cualitativos, qué tipo de variables se presentan como datos discretos, cuáles | ||
| + | pueden entenderse mejor mediante un gráfico de barras, cuáles datos no serían apropiados para este tipo de representación gráfica. Además, los estudiantes | ||
| + | al discutir los datos y su relación con otros elementos del entorno, pueden formular hipótesis o explicaciones y profundizar en el conocimiento de la situación de su municipio o departamento. | ||
| + | |||
| + | 3. Trabajar proyectos ofrece a los estudiantes la oportunidad de acceder a los contenidos desde el ámbito práctico. Los estudiantes obtienen datos a través de observaciones o de encuestas realizadas por ellos mismos. Es necesario que el proyecto a realizar tenga objetivos definidos y fases previamente planificadas que permitan guiar el trabajo, desde el planteamiento del problema a partir de una situación real, hasta la presentación de datos en tablas o gráficos y la generación de conclusiones (revisar Gil y Martín, 2007). Alentar a los estudiantes para que vean la utilidad de las representaciones gráficas para distintos tipos de información, por ejemplo: ¿cuántos hombres y cuántas mujeres hay en el salón de clases?, ¿con qué frecuencia acuden padres de familia al centro de salud?, ¿qué actividades realizan los estudiantes fuera del horario escolar?, ¿cuál es la frecuencia del consumo de distintos tipos de alimento en la comunidad?... | ||
| + | == <span style="color: #e2007a;">Referencias</span> == | ||
| + | <references /> | ||
| + | |||
| + | * DIGECADE –Dirección General de Gestión de Calidad Educativa–. (2010). Curriculum Nacional Base: Bachillerato en Ciencias y Letras. | ||
| + | * Guatemala: Ministerio de Educación. | ||
| + | * DIGECUR – Dirección General de Currículo–. (2013a). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Educación de Productividad y Desarrollo. Guatemala: Ministerio de Educación. | ||
| + | * DIGECUR – Dirección General de Currículo–. (2013b). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Finanzas y Administración. Guatemala: Ministerio de Educación. | ||
| + | * Espinel, M. et al. (2009). Las gráficas estadísticas. En Serrano, L. (Ed.), Tendencias actuales de la investigación en Educación Estocástica. | ||
| + | * Málaga: Universidad de Granada. | ||
| + | * Gil, A. y Martín, J. (2007). La estadística mediante proyectos – Cuaderno de trabajo. Las Palmas de Gran Canaria: Instituto Canario de Estadística. Obtenido desde http://www.gobiernodecanarias.org/istac | ||
| + | * Mendoza, H. & Bautista, G. (2004). Diagrama de barras. Obtenido desde http://www.virtual.unal.edu.co/cursos/ciencias/2001091/html/un3/cont_304_37.html | ||
| + | * USAID –United States Agency for International Development–. (2009). Competencias básicas para la vida. Guatemala: autor. | ||
Revisión del 23:23 8 abr 2015
Estadística
Presentación[editar | editar código]
La evaluación es un elemento fundamental en el modelo de la calidad educativa; sin embargo, por sí misma, no mejora los aprendizajes. Es el uso que se haga de los resultados lo que impacta el alcance de las metas educativas del país. Con el objetivo de facilitar la vinculación de los resultados de la Evaluación Nacional de Graduandos con los procesos de enseñanzaaprendizaje que se dan en el aula, la Dirección General de Evaluación e Investigación Educativa –DIGEDUCA– del Ministerio de Educación, plantea este material como un instrumento para que docentes y directores puedan reflexionar acerca de los resultados obtenidos en el 2013. Se espera que esta reflexión incida en la tarea que cada docente realiza en cualquiera de las áreas curriculares del Nivel de Educación Media, del Ciclo de Educación Diversificada.
Evaluación de Graduandos[editar | editar código]
Anualmente todos los estudiantes que cursan el último año del ciclo diversificado participan en la Evaluación Nacional de Graduandos. El objetivo del proceso es determinar el nivel de los aprendizajes alcanzados por los alumnos al finalizar su paso por el sistema educativo. Para medir las habilidades desarrolladas, se evalúan contenidos declarativos y procedimentales en el contexto de competencias básicas para la vida.
El área curricular de Matemáticas se incluye en la Evaluación Nacional de Graduandos ya que promueve el desarrollo de los procesos cognitivos necesarios para la comprensión cuantitativa de la realidad. Dentro de esta área se consolidan destrezas relacionadas con análisis, razonamiento y comunicación pertinente y eficaz de ideas, a partir del planteamiento, resolución e interpretación de problemas matemáticos (DIGECADE, 2010; DIGECUR, 2013a; DIGECUR, 2013b). Está vinculada directamente con la competencia básica 3: el uso del pensamiento lógico-matemático para la resolución de problemas de la vida cotidiana.
Las pruebas de Matemáticas evalúan contenidos de sistemas numéricos, aritmética, geometría, trigonometría, álgebra, lógica matemática y estadística. En este documento se analizan, desde los procesos cognitivos, errores comunes que los estudiantes evaluados en el 2013 cometieron al resolver ítems de representación gráfica de frecuencias.
|
Conjunto de aprendizajes (conocimientos, procedimientos y actitudes) imprescindibles y fundamentales para que todas las personas se realicen personalmente, se incorporen a la vida adulta de manera satisfactoria y participen activamente como miembros de la sociedad. Cfr. USAID, 2009, p. 5. |
¿Cómo usar este documento?[editar | editar código]
Lea la teoría que sustenta y justifica el contenido evaluado. |
Analice el ítem clonado y su descripción. |
A través del análisis del error, identifique posibles debilidades de los estudiantes. |
Decida estrategias a implementar para contribuir al desarrollo de la competencia matemática. |
|
Resultados El porcentaje de respuestas correctas en estadística fue de 45%. Esto quiere decir que si la prueba incluía 5 ítems que evaluaban este contenido, los estudiantes resolvieron correctamente 2.* *El número de ítems varía en las distintas formas de la prueba. |
Estadística[editar | editar código]
Entre los contenidos específicos de estadística se evalúan los gráficos de barras. Dependiendo del tipo de datos y del objetivo con el que se estén analizando, existen diversas maneras de representar gráficamente la información. La gráfica de barras es útil para representar datos cualitativos o datos cuantitativos discretos. En el eje de las abscisas se colocan los valores de la variable y en el eje de ordenadas, las frecuencias absolutas o relativas. Los datos se representan mediante una altura proporcional a la frecuencia.
Mendoza y Bautista (2004) proponen algunas sugerencias para elaborar este tipo de gráficas:
- Para datos categóricos cualitativos, diseñar las barras en forma horizontal y en forma vertical para datos numéricos discretos.
- Todas las barras deben ser del mismo ancho para no confundir al lector.
- Incluir escalas y títulos para ayudar a la lectura de las gráficas.
- Identificar en forma clara los ejes.
Análisis del ítem[editar | editar código]
Resolver correctamente este ítem evidencia que el estudiante es capaz de reconocer información estadística presentada en gráficas, puede comprender e interpretar los datos representados visualmente.
|
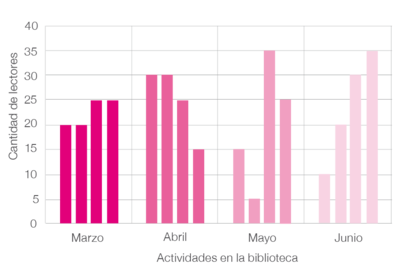
La gráfica muestra el número de lectores que asistieron a distintas actividades de la biblioteca. ¿Qué mes tuvo un mayor promedio de asistencia? a. Marzo b. Abril c. Mayo d. Junio |
| Competencia básica 3: Pensamiento lógico-matemático | |
| Dimensión clave | Conocimiento y manejo de los elementos matemáticos básicos. |
| Componente | Integración y aplicación de conocimientos estadísticos. |
| Indicador de logro | Explica la información que presentan diferentes tipos de gráficas. |
| Contenido evaluado | Uso de gráfico de barras |
| Demanda cognitiva | Comprensión |
| Respuesta correcta | Opción b |
Análisis del error[editar | editar código]
Si seleccionaron la opción a, los estudiantes no identificaron que marzo fue uno de los meses en que el promedio de asistencia fue menor. Omitieron información de la gráfica como un rango pequeño, valores similares y un valor máximo (25) menor a los valores máximos observados en otros meses.
Quienes eligieron la opción c o la opción d probablemente observaron el valor máximo de lectores que asistieron a las actividades de la biblioteca esos meses (35), pero no reconocieron que el promedio se ve afectado por valores mínimos y máximos extremos, como se observa en las barras de mayo y junio; ambos meses tienen un rango amplio de frecuencia.
Si los estudiantes no dominan conceptos de medidas de tendencia central, no podrán interpretar de manera adecuada gráficos que las ilustran. No necesitan calcular el promedio de cada mes; con identificar que la gráfica ilustra igual cantidad de actividades en cada mes, podrían calcular la frecuencia total de lectores que asiste mensualmente y con ello inferir el mes con una media mayor. Esto no resulta posible si hay una debilidad en la comprensión del concepto y cálculo de un promedio de datos.
Sugerencias de estrategias de enseñanza-aprendizaje[editar | editar código]
|
La comprensión de los gráficos es la habilidad que permite a los estudiantes obtener información a partir de un gráfico creado por ellos mismos o por otros. Esta comprensión puede darse en tres niveles que deben procurarse en la enseñanza de la estadística: racional/literal –leer los datos–, crítico –leer entre datos– e hipotético –leer más allá de los datos– (Espinel et. al, 2009). |
1. Buscar en periódicos y medios de comunicación gráficos de barras, utilizarlos para identificar elementos gráficos, para analizar la claridad de la información presentada, el contexto de los datos, el objetivo del gráfico en la comunicación.
2. Favorecer el uso de información disponible sobre la comunidad. Pueden ser datos sobre encuestas nacionales, datos de salud, indicadores educativos, indicadores municipales, etc. Contar con datos reales del contexto propio favorecerá el significado que se dé a los aprendizajes. Los estudiantes pueden identificar en esta información, qué tipo de variables se presentan como datos cualitativos, qué tipo de variables se presentan como datos discretos, cuáles pueden entenderse mejor mediante un gráfico de barras, cuáles datos no serían apropiados para este tipo de representación gráfica. Además, los estudiantes al discutir los datos y su relación con otros elementos del entorno, pueden formular hipótesis o explicaciones y profundizar en el conocimiento de la situación de su municipio o departamento.
3. Trabajar proyectos ofrece a los estudiantes la oportunidad de acceder a los contenidos desde el ámbito práctico. Los estudiantes obtienen datos a través de observaciones o de encuestas realizadas por ellos mismos. Es necesario que el proyecto a realizar tenga objetivos definidos y fases previamente planificadas que permitan guiar el trabajo, desde el planteamiento del problema a partir de una situación real, hasta la presentación de datos en tablas o gráficos y la generación de conclusiones (revisar Gil y Martín, 2007). Alentar a los estudiantes para que vean la utilidad de las representaciones gráficas para distintos tipos de información, por ejemplo: ¿cuántos hombres y cuántas mujeres hay en el salón de clases?, ¿con qué frecuencia acuden padres de familia al centro de salud?, ¿qué actividades realizan los estudiantes fuera del horario escolar?, ¿cuál es la frecuencia del consumo de distintos tipos de alimento en la comunidad?...
Referencias[editar | editar código]
- DIGECADE –Dirección General de Gestión de Calidad Educativa–. (2010). Curriculum Nacional Base: Bachillerato en Ciencias y Letras.
- Guatemala: Ministerio de Educación.
- DIGECUR – Dirección General de Currículo–. (2013a). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Educación de Productividad y Desarrollo. Guatemala: Ministerio de Educación.
- DIGECUR – Dirección General de Currículo–. (2013b). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Finanzas y Administración. Guatemala: Ministerio de Educación.
- Espinel, M. et al. (2009). Las gráficas estadísticas. En Serrano, L. (Ed.), Tendencias actuales de la investigación en Educación Estocástica.
- Málaga: Universidad de Granada.
- Gil, A. y Martín, J. (2007). La estadística mediante proyectos – Cuaderno de trabajo. Las Palmas de Gran Canaria: Instituto Canario de Estadística. Obtenido desde http://www.gobiernodecanarias.org/istac
- Mendoza, H. & Bautista, G. (2004). Diagrama de barras. Obtenido desde http://www.virtual.unal.edu.co/cursos/ciencias/2001091/html/un3/cont_304_37.html
- USAID –United States Agency for International Development–. (2009). Competencias básicas para la vida. Guatemala: autor.
Indicadores de éxito de un plan escrito en forma específica.
Conjunto de aprendizajes (conocimientos, procedimientos y actitudes) imprescindibles y fundamentales para que todas las personas se realicen personalmente, se incorporen a la vida adulta de manera satisfactoria y participaen activamente como miembros de la sociedad.
Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario
En el sistema cartesiano, se dice de la coordenada vertical.
Sacar una consecuencia o deducir algo de otra cosa.
Capacidad o destreza para hacer algo bien o con facilidad.