8
| (No se muestran 10 ediciones intermedias de 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | <span style="font-size:200%;;color: #ff0088">Geometría: áreas y perímetros</span | + | {{#TwitterFBLike:right|like}}<span style="font-size:200%;;color: #ff0088">Geometría: áreas y perímetros</span> |
[[Archivo:AREA_Y_PERIMETRO-2.png|900px]] | [[Archivo:AREA_Y_PERIMETRO-2.png|900px]] | ||
| + | |||
== <span style="color: #ff0088;">Presentación</span> == | == <span style="color: #ff0088;">Presentación</span> == | ||
| − | <span style="color: #ff0088;">La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del | + | <div style="float:right">__TOC__</div> |
| + | |||
| + | <span style="color: #ff0088;">La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.</span><br /> | ||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| | | | ||
| Línea 9: | Línea 12: | ||
| | | | ||
<center>'''OBJETIVOS'''</center> | <center>'''OBJETIVOS'''</center> | ||
| − | * Analizar desde los procesos cognitivos los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del | + | * Analizar desde los procesos cognitivos, los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del Ciclo de Educación Básica del Nivel de Educación Media. |
* Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes. | * Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes. | ||
|} | |} | ||
|} | |} | ||
== <span style="color: #ff0088;">¿Cómo usar este documento?</span> == | == <span style="color: #ff0088;">¿Cómo usar este documento?</span> == | ||
| − | Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar | + | Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Ciclo de Educación Básica del Nivel de Educación Media. |
| − | el proceso de aprendizaje de los estudiantes del | + | |
| − | En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta el aprendizaje de | + | En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta el aprendizaje del cálculo de áreas y perímetros de figuras geómetricas. A continuación, se presenta un ítem clonado de la prueba de Matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad de que el docente ubique el contenido evaluado dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza que apoya el desarrollo de la competencia matemática y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional. |
| − | DIGEDUCA, con la finalidad de que el docente ubique el contenido dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza que apoya el desarrollo de la competencia matemática y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional. | + | |
| − | En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. | + | En el apartado '''Análisis del error''', se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. |
| − | Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y | + | |
| − | promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los | ||
| − | aprendizajes, que desde luego no quedan agotadas en este bifoliar. | ||
| − | Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. | ||
La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país. | La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país. | ||
== <span style="color: #ff0088;">Geometría: áreas y perímetros</span> == | == <span style="color: #ff0088;">Geometría: áreas y perímetros</span> == | ||
El perímetro de una figura geométrica plana es la medida longitudinal de su contorno. En general, para calcular el perímetro se suman las medidas de todos los lados de la figura, excepto en el círculo. El perímetro de un círculo se llama circunferencia. El área de una figura geométrica plana es la medida de la superficie que ocupa. Para medir una superficie se toma como unidad un cuadrado cuyo lado sea igual a la unidad de longitud. Considere que en la siguiente figura cada cuadrado tiene un 1.00 cm de lado, entonces el perímetro y el área de la figura indicada es: | El perímetro de una figura geométrica plana es la medida longitudinal de su contorno. En general, para calcular el perímetro se suman las medidas de todos los lados de la figura, excepto en el círculo. El perímetro de un círculo se llama circunferencia. El área de una figura geométrica plana es la medida de la superficie que ocupa. Para medir una superficie se toma como unidad un cuadrado cuyo lado sea igual a la unidad de longitud. Considere que en la siguiente figura cada cuadrado tiene un 1.00 cm de lado, entonces el perímetro y el área de la figura indicada es: | ||
<center>[[Archivo:Fig1-AREA_Y_PERIMETRO-2.png |350px|Tabla 1.]]</center> | <center>[[Archivo:Fig1-AREA_Y_PERIMETRO-2.png |350px|Tabla 1.]]</center> | ||
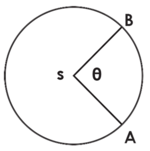
| − | Para medir la longitud de una circunferencia y el área debe de identificar el radio del círculo y emplear para el cálculo las expresiones C = 2π r y A = π r<sup>2</sup>. Para determinar el perímetro o el área de una sección del círculo se debe de identificar el ángulo central del círculo con vértice en el centro del círculo. Los ángulos se pueden medir en grados o radianes. La medida en radianes correspondiente a 360º es 2π. Sí 0 es el ángulo central, como se muestra en la figura, se dice que la longitud del arco AB del círculo, denominado '''s''', subtiende a 0. Si un arco de longitud '''s''' de un circulo de radio '''r''' subtiende un ángulo central de 0 radianes, entonces s = r ∙ 0 y sí A es el área del sector circular determinado por 0 entonces A= | + | Para medir la longitud de una circunferencia y el área debe de identificar el radio del círculo y emplear para el cálculo las expresiones C = 2π r y A = π r<sup>2</sup>. Para determinar el perímetro o el área de una sección del círculo se debe de identificar el ángulo central del círculo con vértice en el centro del círculo. Los ángulos se pueden medir en grados o radianes. La medida en radianes correspondiente a 360º es 2π. Sí 0 es el ángulo central, como se muestra en la figura, se dice que la longitud del arco AB del círculo, denominado '''s''', subtiende a 0. Si un arco de longitud '''s''' de un circulo de radio '''r''' subtiende un ángulo central de 0 radianes, entonces s = r ∙ 0 y sí A es el área del sector circular determinado por 0 entonces [[Archivo:AREA_Y_PERIMETRO-2_figurita1.png|70px]] |
| + | <center>[[Archivo:Fig2-AREA_Y_PERIMETRO-2.png |150px|]]</center> | ||
| + | == <span style="color: #ff0088;">Análisis del ítem</span> == | ||
| + | Al incluir ítems de áreas y perímetros se espera que el estudiante evidencie que comprende los cálculos que son necesarios para resolver el área de un sector. | ||
| + | <center>[[Archivo:Fig3-AREA_Y_PERIMETRO-2.png |350px|]]</center> | ||
| + | <center>[[Archivo:Fig4-AREA_Y_PERIMETRO-2x.png |350px|]]</center> | ||
| + | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="50%" | ||
| + | | <span style="color: #ffffff;"><center>Porcentaje de respuestas correctas en los ítems que evalúan área de figuras geométricas. '''25,0%'''</center></span> | ||
| + | |} | ||
| + | La demanda cognitiva de este ítem, ubicada en utilización, requiere del estudiante '''identificar aplicaciones específicas o consecuencias lógicas del conocimiento.''' | ||
| + | == <span style="color: #ff0088;">Análisis del error</span> == | ||
| + | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| + | | | ||
| + | {| style="background:White;border:2px solid White;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="95%" | ||
| + | | | ||
| + | Previo a la enseñanza de áreas del sector de un círculo debe reforzar los siguientes conocimientos básicos: | ||
| + | # Cálculo de perímetros y áreas de las siguientes figuras planas: cuadrado, rectángulo, triángulo, trapecio, rombo, romboide. | ||
| + | # Definición del número irracional π | ||
| + | # Calculo de la longitud de la circunferencia y área del círculo. | ||
| + | # Conversión de grados a radianes y viceversa. | ||
| + | |} | ||
| + | |} | ||
| + | <center>[[Archivo: AREA_Y_PERIMETRO_figurax.png |500px|]]</center> | ||
| + | Los posibles errores cometidos por los estudiantes son los siguientes: Si el estudiante eligió la opción…<br /> | ||
| + | a. identifica que el área sombreada tiene un ángulo de 225° y que el radio del círculo es de 10 cm; pero considera incorrectamente que estas dos medidas son las dimensiones necesarias para el cálculo del área y las multiplica.<br /> | ||
| + | b. debido a una lectura incorrecta del problema elige el ángulo del área no sombreada con valor de 135° y lo expresa en radianes obteniendo[[Archivo:Fitura_tres_cuartos.png|25px]] π calculando así el área del sector circular no sombreada con un valor de:[[Archivo:Figura_siete_dos.png|25px]] π cm2<br /> | ||
| + | c. expresa el ángulo de 225° correctamente en radianes y obtiene [[Archivo:Figurita_cinco_cuatro.png |30px|]] pero este resultado lo multiplica por 10 cm y obtiene 12.5 π, que representa la longitud del arco y no el área de la región sombreada. | ||
| + | {| style="border:2px solid #ff0088;border-radius: 4px;padding:8px; font-size:130%; line-height:1.2; margin:1em auto 1em auto" width="65%" | ||
| + | | | ||
| + | En conclusión, los errores evidencian que no tiene conocimiento para determinar el área de un sector circular. | ||
| + | |} | ||
| + | |||
| + | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| + | | | ||
| + | {| style="background:White;border:2px solid White;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="95%" | ||
| + | | | ||
| + | En el CNB la [[Malla curricular de Matemáticas - Tercer Grado#Escrito|competencia 1]] expresa que el estudiante “Produce patrones aritméticos, algebraicos y geométricos, aplicando propiedades y relaciones.”. Para ello, se propone como indicador de logro la resolución problemas que involucran cálculo de medidas y aplicación de propiedades de figuras planas y cuerpos sólidos. Los contenidos declarativos y procedimentales que permitirán desarrollar la competencia prevista son: Aplicación de las medidas para calcular perímetro, área y volumen. Trazo del círculo y de sus segmentos con instrumentos geométricos. Clasificación de los ángulos en el círculo. Círculo y segmentos asociados. | ||
| + | <ref>Curriculum Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado. (2010), p. 49.</ref> | ||
| + | |} | ||
| + | |} | ||
| + | == <span style="color: #ff0088;">Sugerencias de estrategias de aprendizaje</span> == | ||
| + | 1. Calculen el perímetro y área de figuras geométricas compuestas. Oriéntelos para que dividan las figuras en cuadrados, rectángulos, triángulos, etc. para determinar el perímetro y área total de la figura. El ejemplo siguiente le sirve de guía: | ||
| + | |||
| + | ¿Cuál es el área total de la figura? | ||
| + | [[Archivo:Fig5-AREA_Y_PERIMETRO-2.png|350px]] | ||
| + | |||
| + | La respuesta es: 34.57 U<sup>2</sup> | ||
| + | |||
| + | A = 16 U<sup>2</sup> + 6 U<sup>2</sup> + 4π U<sup>2</sup><br /> | ||
| + | |||
| + | Para esta situación se empleo la aproximación de π = 3.1416 | ||
| + | |||
| + | 2. Recorten 5 círculos de cartón de diferentes diámetros, luego midan la longitud de la circunferencia y el área del círculo. Elijan un círculo de cartón y usando el transportador midan un ángulo central de 60° grados, por ejemplo; encuentren el área del sector y la longitud de arco respectivo. | ||
| + | 3. Establezcan el valor aproximado de π : recorten 8 círculos de diferente tamaño, midan la circunferencia y diámetro de cada uno. Usen una cuerda para medir la circunferencia. Luego dividan C/D para cada caso, los valores obtenidos deben de tener una tendencia a 3 y no ser mayores que 3.30, discutan los resultados. Con esta actividad definen el valor de π y el concepto de radian. | ||
| + | 4. Utilicen un círculo para representar las medidas de ángulos en radianes y grados, como en el siguiente ejemplo. | ||
| + | <center>[[Archivo:Figura_de_area_y_perimetrol.png|600px]]</center> | ||
| + | == <span style="color: #ff0088;">Referencias</span> == | ||
| + | <references /> | ||
| + | '''Documentos digitales'''<br /> | ||
| + | * Swokowsky, E.W y Cole, J.A. (1998). Algebra y Trigonometría. 9ed. International Thomson Editores. México. Pag.500-508 | ||
| + | * Rodríguez, J. Caraballo, A. Cruz, T. Hernández O.(1997). Razonamiento Matemático. Fundamentosy aplicaciones. Thomson Editores SA. México. Pag. 67-96. | ||
| + | '''Fuentes electrónicas:''' | ||
| + | * Aula fácil. Matemática. Cálculo de áreas geométricas. Documento recuperado el 8 de junio de 2012: http://www.aulafacil.com/matematicas-areasgeometria/curso/Temario.htm | ||
| + | |||
| + | [[Category:Matemáticas]] [[Category:Básico]] [[Categoría:Resultados de las evaluaciones]][[Category:Book:Serie_aprender_del_error]] | ||
Revisión actual del 12:10 8 nov 2014
Geometría: áreas y perímetros
Presentación[editar | editar código]
La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.
|
¿Cómo usar este documento?[editar | editar código]
Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Ciclo de Educación Básica del Nivel de Educación Media.
En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta el aprendizaje del cálculo de áreas y perímetros de figuras geómetricas. A continuación, se presenta un ítem clonado de la prueba de Matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad de que el docente ubique el contenido evaluado dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza que apoya el desarrollo de la competencia matemática y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional.
En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida.
La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país.
Geometría: áreas y perímetros[editar | editar código]
El perímetro de una figura geométrica plana es la medida longitudinal de su contorno. En general, para calcular el perímetro se suman las medidas de todos los lados de la figura, excepto en el círculo. El perímetro de un círculo se llama circunferencia. El área de una figura geométrica plana es la medida de la superficie que ocupa. Para medir una superficie se toma como unidad un cuadrado cuyo lado sea igual a la unidad de longitud. Considere que en la siguiente figura cada cuadrado tiene un 1.00 cm de lado, entonces el perímetro y el área de la figura indicada es:
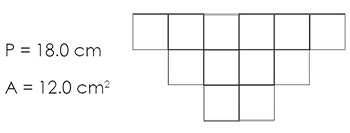
Para medir la longitud de una circunferencia y el área debe de identificar el radio del círculo y emplear para el cálculo las expresiones C = 2π r y A = π r2. Para determinar el perímetro o el área de una sección del círculo se debe de identificar el ángulo central del círculo con vértice en el centro del círculo. Los ángulos se pueden medir en grados o radianes. La medida en radianes correspondiente a 360º es 2π. Sí 0 es el ángulo central, como se muestra en la figura, se dice que la longitud del arco AB del círculo, denominado s, subtiende a 0. Si un arco de longitud s de un circulo de radio r subtiende un ángulo central de 0 radianes, entonces s = r ∙ 0 y sí A es el área del sector circular determinado por 0 entonces ![]()
Análisis del ítem[editar | editar código]
Al incluir ítems de áreas y perímetros se espera que el estudiante evidencie que comprende los cálculos que son necesarios para resolver el área de un sector.
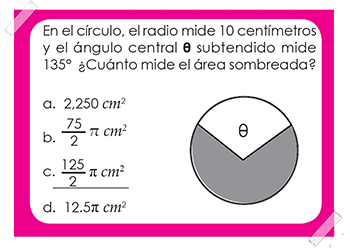
La demanda cognitiva de este ítem, ubicada en utilización, requiere del estudiante identificar aplicaciones específicas o consecuencias lógicas del conocimiento.
Análisis del error[editar | editar código]
|

Los posibles errores cometidos por los estudiantes son los siguientes: Si el estudiante eligió la opción…
a. identifica que el área sombreada tiene un ángulo de 225° y que el radio del círculo es de 10 cm; pero considera incorrectamente que estas dos medidas son las dimensiones necesarias para el cálculo del área y las multiplica.
b. debido a una lectura incorrecta del problema elige el ángulo del área no sombreada con valor de 135° y lo expresa en radianes obteniendo![]() π calculando así el área del sector circular no sombreada con un valor de:
π calculando así el área del sector circular no sombreada con un valor de:![]() π cm2
π cm2
c. expresa el ángulo de 225° correctamente en radianes y obtiene ![]() pero este resultado lo multiplica por 10 cm y obtiene 12.5 π, que representa la longitud del arco y no el área de la región sombreada.
pero este resultado lo multiplica por 10 cm y obtiene 12.5 π, que representa la longitud del arco y no el área de la región sombreada.
|
En conclusión, los errores evidencian que no tiene conocimiento para determinar el área de un sector circular. |
|
Sugerencias de estrategias de aprendizaje[editar | editar código]
1. Calculen el perímetro y área de figuras geométricas compuestas. Oriéntelos para que dividan las figuras en cuadrados, rectángulos, triángulos, etc. para determinar el perímetro y área total de la figura. El ejemplo siguiente le sirve de guía:
¿Cuál es el área total de la figura?
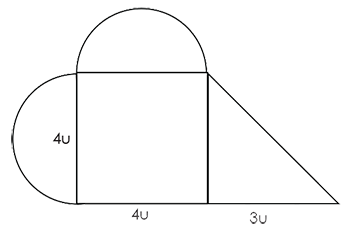
La respuesta es: 34.57 U2
A = 16 U2 + 6 U2 + 4π U2
Para esta situación se empleo la aproximación de π = 3.1416
2. Recorten 5 círculos de cartón de diferentes diámetros, luego midan la longitud de la circunferencia y el área del círculo. Elijan un círculo de cartón y usando el transportador midan un ángulo central de 60° grados, por ejemplo; encuentren el área del sector y la longitud de arco respectivo. 3. Establezcan el valor aproximado de π : recorten 8 círculos de diferente tamaño, midan la circunferencia y diámetro de cada uno. Usen una cuerda para medir la circunferencia. Luego dividan C/D para cada caso, los valores obtenidos deben de tener una tendencia a 3 y no ser mayores que 3.30, discutan los resultados. Con esta actividad definen el valor de π y el concepto de radian. 4. Utilicen un círculo para representar las medidas de ángulos en radianes y grados, como en el siguiente ejemplo.

Referencias[editar | editar código]
- ↑ Curriculum Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado. (2010), p. 49.
Documentos digitales
- Swokowsky, E.W y Cole, J.A. (1998). Algebra y Trigonometría. 9ed. International Thomson Editores. México. Pag.500-508
- Rodríguez, J. Caraballo, A. Cruz, T. Hernández O.(1997). Razonamiento Matemático. Fundamentosy aplicaciones. Thomson Editores SA. México. Pag. 67-96.
Fuentes electrónicas:
- Aula fácil. Matemática. Cálculo de áreas geométricas. Documento recuperado el 8 de junio de 2012: http://www.aulafacil.com/matematicas-areasgeometria/curso/Temario.htm
Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario
Habilidad, facilidad o arte para hacer algo bien hecho.
En el continuo de coaching es el rol de ser muy directo y enseñar, mostrar, guiar, etc.
