Área de Matemáticas
m (Editor trasladó la página Orientaciones curriculares primaria 2022/Tercero Básico/Área de Matemáticas a Orientaciones curriculares 2022/Tercero Básico/Área de Matemáticas sin dejar una redirección: Aclarar título) |
|||
| (No se muestran 5 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
| + | <center><div style="background-color:#e4f6ff; width:50%; border-radius:10px; padding:5px; float:right">[[Currículo Emergente - Tablas de Alcance y Secuencia 2022/{{#titleparts: {{BASEPAGENAME}} | 2 | 2 }}/{{SUBPAGENAME}}|Consulta las tablas de alcance y secuencia para {{#titleparts: {{BASEPAGENAME}} | 2 | 2 }} aquí]]</div></center> | ||
==Sobre el área curricular de Matemáticas== | ==Sobre el área curricular de Matemáticas== | ||
Esta área complementa a otras dentro del currículo, para propiciar el desarrollo del pensamiento científico y lógico, por lo que está enfocada en perfeccionar habilidades de cálculo, estimación, representación, argumentación, predicción, comunicación en un lenguaje propio y la demostración, que son necesarias en todo el proceso de formación integral. | Esta área complementa a otras dentro del currículo, para propiciar el desarrollo del pensamiento científico y lógico, por lo que está enfocada en perfeccionar habilidades de cálculo, estimación, representación, argumentación, predicción, comunicación en un lenguaje propio y la demostración, que son necesarias en todo el proceso de formación integral. | ||
| Línea 38: | Línea 39: | ||
===Unidad 3=== | ===Unidad 3=== | ||
| + | <div style="background:#f9ccdf; width:95%; padding:8px; margin:1.5em auto 1em auto;> | ||
| + | <center>'''Matemáticas'''</center> | ||
| + | </div> | ||
| + | <center>Eje: Desarrollo tecnológico</center> | ||
| + | {|class="wikitable" style="width:95%; margin:1em auto 1em auto;" | ||
| + | |colspan="2" style="background:#fbdfeb; text-align:center;"|'''PERÍODOS''' | ||
| + | |style="background:#fbdfeb; text-align:center; width:15%;"|'''1''' | ||
| + | |style="background:#fbdfeb; text-align:center; width:15%;"|'''2''' | ||
| + | |style="background:#fbdfeb; text-align:center; width:15%;"|'''3''' | ||
| + | |style="background:#fbdfeb; text-align:center; width:15%;"|'''4''' | ||
| + | |style="background:#fbdfeb; text-align:center; width:15%;"|'''5''' | ||
| + | |-valign="top" | ||
| + | |colspan="2" style="background:#f9ccdf; text-align:center;"|'''MODALIDAD''' | ||
| + | |style="background:#fcf4cb; text-align:center;"|A distancia | ||
| + | |style="background:#fff79a; text-align:center;"|Presencial | ||
| + | |style="background:#fcf4cb; text-align:center;"|A distancia | ||
| + | |style="background:#fcf4cb; text-align:center;"|A distancia | ||
| + | |style="background:#fcf4cb; text-align:center;"|A distancia | ||
| + | |-valign="top" | ||
| + | |rowspan="2" style="background:#fbdfeb; writing-mode: vertical-rl; transform: rotate(180deg); width=5px; text-align:center;"|<big>'''Contenido'''</big> | ||
| + | |style="background:#fbdfeb;"|Según la dosificación | ||
| + | |Factorización | ||
| + | |Factorización | ||
| + | |Factorización | ||
| + | |Factorización | ||
| + | |Factorización | ||
| + | |-valign="top" | ||
| + | |style="background:#fbdfeb;"|'''Currículo emergente''' | ||
| + | |1.1.4.1 | ||
| + | |1.1.4.2 | ||
| + | |1.1.4.4 | ||
| + | |1.1.4.4 | ||
| + | |1.1.4.3 | ||
| + | |-valign="top" | ||
| + | |rowspan="3" style="background:#fbdfeb; writing-mode: vertical-rl; transform: rotate(180deg); width=5px; text-align:center;"|<big>'''Pasos del aprendizaje'''</big> | ||
| + | |style="background:#fbdfeb;"|1. Exploración de conocimientos previos (''libro Matemática'') | ||
| + | |Construcción con material manipulativo de expresiones '''Página 13''' | ||
| + | |Indagación sobre expresiones que representan cuadros | ||
| + | |Caracterización de los trinomios | ||
| + | |Reflexión: ¿Qué pasa si no es trinomio cuadrado perfecto? | ||
| + | |Reflexión: ¿cómo se construye un cubo?, ¿cómo son las caras de un cubo?, ¿cómo se representan matemáticamente estas situaciones? | ||
| + | |-valign="top" | ||
| + | |style="background:#fbdfeb;"|2. Nuevos conocimientos(''libro Matemática'') | ||
| + | |Factor común, '''página 14''' | ||
| + | |Diferencia de cuadrados, página 20 | ||
| + | |Trinomios, concepto de trinomio cuadrado perfecto, '''página 16''' | ||
| + | |Trinomios, otro tipo de trinomios, '''página 22''' | ||
| + | |Suma y diferencia de cubos | ||
| + | |-valign="top" | ||
| + | |style="background:#fbdfeb;"|3. Integración/evaluación (''libro Matemática'') | ||
| + | |Reconocimiento de los factores común en las expresiones algebraicas | ||
| + | |Aplicación de factor común y diferencia de cuadrados, '''página 26''' | ||
| + | |Factor común y trinomio cuadrado perfecto, '''página 18''' | ||
| + | |Aplicación de los diferentes trinomios cuando cambian los signos de un término, '''página 24''' | ||
| + | |Solución a cuestiones y problemas: ¿Cómo se representa el volumen de un cubo con una expresión algebraica? ¿Qué implica agregar un cubo?, ¿qué implica quitar un cubo? | ||
| + | |} | ||
| + | |||
| + | ==b. Modelaje de sesión de clases== | ||
| + | '''Clase presencial -Sesión 2''' | ||
| + | |||
| + | ===Paso 1: Exploración de conocimientos previos=== | ||
| + | Recorte cuadrados y rectángulos de papel para representar las expresiones que se presentan en la página 13 del libro ''Matemática''. | ||
| + | |||
| + | Solicite a los estudiantes, a manera de juego, que construyan las expresiones que usted proponga; verifique que estas sean correctas y aproveche a corregir lo que sea necesario. En esta etapa del aprendizaje se trata de recordar o bien practicar un concepto para poder conectarlo con los siguientes. Con esta actividad se puede verificar que el estudiante utilice conocimientos previos como argumento de su razonamiento. | ||
| + | |||
| + | ===Paso 2: Nuevos conocimientos=== | ||
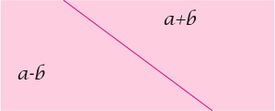
| + | El tema principal de esta sesión es la diferencia de cuadrados. Este tema se presta para la construcción geométrica de forma concreta, por lo que puede solicitar a los estudiantes que construyan un cuadrado de aproximadamente 10 cm de lado y le corten un cuadrado de 2 cm de lado en una de sus esquinas. Luego, deberán hacer el arreglo para construir un rectángulo que represente la expresión (x+a) (x-a), que, para este cuadrado queda así: (10+2) (10-2). | ||
| + | |||
| + | Con esto, justifique la expresión coloquial de: «… una vez sumando y otra, restando». En esta etapa es importante comprender que la factorización sirve como otra forma de representación algebraica de una misma situación: x<sup>2</sup>-a<sup>2</sup>=(x+a) (x-a). Para reconocer el algoritmo puede utilizar la página 20 del libro Matemática. | ||
| + | |||
| + | ===Paso 3: Integración-evaluación=== | ||
| + | Utilice la actividad de la página 26 para provocar reflexión sobre ¿qué sucede si a la expresión se le antepone un número? Esto permitirá la integración de conceptos. También puede utilizar la página 21 para practicar el algoritmo. | ||
| + | |||
| + | Agregue actividades de construcción de la factorización con cuadrados de diferentes medidas. Estas actividades pueden realizarse de forma colaborativa, en parejas —siempre con las medidas sanitarias pertinentes—, con el fin de discutir la temática propuesta. Este tipo de actividades permite evaluar el proceso de aprendizaje de los estudiantes. | ||
| + | |||
| + | Criterios de evaluación: según el currículo emergente para esta sesión se espera que el estudiante demuestre que '''«representa la factorización de diferencia de cuadrados en la geometría»'''. | ||
| + | |||
| + | <div style="width:65%; margin:1em auto 5em auto;"> | ||
| + | <div style="width: 40%; float:left"> | ||
| + | [[Archivo:Orientaciones Tercero Básico pag(32.1).jpg|165px|center]] | ||
| + | </div> | ||
| + | <div style="width:50%; float:right;"> | ||
| + | [[Archivo:Orientaciones Tercero Básico pag(32.2).jpg|275px|center]] | ||
| + | </div> | ||
| + | </div><div style="clear: both"></div> | ||
| + | |||
| + | [[Categoría: Matemáticas]] | ||
Revisión actual del 22:11 12 jul 2022
Sobre el área curricular de Matemáticas[editar | editar código]
Esta área complementa a otras dentro del currículo, para propiciar el desarrollo del pensamiento científico y lógico, por lo que está enfocada en perfeccionar habilidades de cálculo, estimación, representación, argumentación, predicción, comunicación en un lenguaje propio y la demostración, que son necesarias en todo el proceso de formación integral.
En el currículo emergente propuesto para el 2022, se busca el fortalecimiento de las mismas competencias e indicadores de logro para el área de Matemáticas del Currículo Nacional Base. Únicamente se realizó la priorización en cuanto a los contenidos, de tal forma que los aprendizajes puntuales permitan el alcance de dichas competencias. Se propone criterios de evaluación para estos contenidos, ya que estos son la guía para verificar y determinar si se está alcanzando el aprendizaje, o bien para replantear hacia dónde encaminar las siguientes acciones. En este currículo también se sugiere una dosificación del número de sesiones de aprendizaje.
Es importante mencionar que, en el Nivel de Educación Media, Ciclo Básico de la educación guatemalteca, la intención metodológica del área de Matemáticas parte del contexto del estudiante, por lo que los procesos aritméticos se convierten en la base que permite la construcción de los conceptos algebraicos (la generalización). Esto implica que, en los primeros años de este ciclo, la aritmética se aborde en un alto porcentaje del tiempo. Conforme se avanza en los grados, estos aprendizajes disminuyen (aunque no se eliminan), y se prioriza más el aprendizaje de las estructuras, relaciones y representaciones abstractas, el cual se aborda poco en los primeros grados.
Es necesario establecer referentes de trabajo para el área curricular de Matemáticas, por lo que se pretende alinearla a los ejes curriculares que se describen en la parte 1 del Currículo Nacional Base. Estos se pueden encontrar, para una mayor comprensión, en el CNB de cualquier grado del Nivel de Educación Primaria y servirán como un horizonte en el desarrollo temático, enumerando algunos de ellos, tenemos: Educación en valores, Desarrollo tecnológico, Multiculturalidad e interculturalidad, Equidad de género, etnia y social, entre otros.
Los aprendizajes en tercer grado ciclo básico[editar | editar código]
En este grado se pretende que el estudiante fortalezca su comunicación matemática, tanto en lectura como en escritura, la cual le permitirá realizar la descripción del contexto en cuanto a formas, patrones, cantidades (sus representaciones y sus relaciones); por lo que el proceso de abstracción matemática es de suma importancia y será fortalecido a partir del manejo de material concreto, pues esto posibilitará la conceptualización a partir de la experiencia.
Con este fin y, atendiendo a la situación actual, en la unidad 1 se enfatiza en conocimientos que se debieron adquirir en segundo básico, para asegurar el andamiaje en la construcción de los aprendizajes específicos para tercero básico. Para ello será necesaria una revisión preliminar de los conceptos presentados en esta unidad, así como de lo que encontrará en el texto, para abordarlos con menor gradualidad de la que corresponde a tercero básico para fortalecerlos y así asegurar su aprendizaje.
La planificación[editar | editar código]
Al momento de planificar las sesiones de aprendizaje se sugiere establecer una metodología que permita el desarrollo del proceso de aprendizaje, por ejemplo, la de «aula inversa o flipped classroom», para lo cual se plantean los siguientes pasos:
1. Planifique Utilice la unidad que corresponde a dicha planificación según el currículo emergente. Organice los aprendizajes alineados a un tema del área de Matemáticas en relación con uno de los ejes curriculares, con el fin de lograr la contextualización.
2. Seleccione Ubique en el libro Matemática de tercero básico de la serie Guatemática, los contenidos que pueden complementar el tema seleccionado para lograr un aprendizaje significativo.
3. Diseñe actividades de aprendizaje Estas deben ser secuenciales y graduales para lograr el aprendizaje esperado en función de los indicadores de logro. Con estas actividades, elabore materiales que puedan trabajarse a distancia y que complementen las páginas del libro Matemática para que puedan ser entregadas o enviadas a los estudiantes o padres de familia.
4. Evalúe las competencias de los estudiantes por medio de diferentes herramientas: diseñe actividades que permitan verificar el progreso de los aprendizajes según los criterios de evaluación propuestos en las sesiones. En estas actividades se puede verificar el aprendizaje aplicando instrumentos (rúbricas, listas de cotejo, entre otros) que le permitan identificar el avance de los estudiantes. Promueva la participación de los estudiantes en el proceso de evaluación (autoevaluación, coevaluación y heteroevaluación).
5. Proponga sesiones de aprendizaje que promuevan el trabajo colaborativo: para ser aplicadas de forma presencial con el resguardo debido en función de la salud, pero que permitan fortalecer el estado emocional de los estudiantes.
A continuación, se presenta un modelaje en el que podrá visualizar los períodos que contemplan modalidad presencial y a distancia, en el que se ejemplifican las actividades cuya efectividad en el aprendizaje es más factible de forma presencial y se definen las actividades que los estudiantes pueden realizar de forma independiente trabajando a distancia, de manera que se logren los aprendizajes esperados; por ello, es importante que siga este modelo al realizar la planificación de los períodos de clase.
a. Modelaje de planificación semanal[editar | editar código]
1. Resuelve problemas utilizando las relaciones y propiedades entre patrones algebraicos, geométricos y trigonométricos.
Unidad 3[editar | editar código]
| PERÍODOS | 1 | 2 | 3 | 4 | 5 | |
| MODALIDAD | A distancia | Presencial | A distancia | A distancia | A distancia | |
| Contenido | Según la dosificación | Factorización | Factorización | Factorización | Factorización | Factorización |
| Currículo emergente | 1.1.4.1 | 1.1.4.2 | 1.1.4.4 | 1.1.4.4 | 1.1.4.3 | |
| Pasos del aprendizaje | 1. Exploración de conocimientos previos (libro Matemática) | Construcción con material manipulativo de expresiones Página 13 | Indagación sobre expresiones que representan cuadros | Caracterización de los trinomios | Reflexión: ¿Qué pasa si no es trinomio cuadrado perfecto? | Reflexión: ¿cómo se construye un cubo?, ¿cómo son las caras de un cubo?, ¿cómo se representan matemáticamente estas situaciones? |
| 2. Nuevos conocimientos(libro Matemática) | Factor común, página 14 | Diferencia de cuadrados, página 20 | Trinomios, concepto de trinomio cuadrado perfecto, página 16 | Trinomios, otro tipo de trinomios, página 22 | Suma y diferencia de cubos | |
| 3. Integración/evaluación (libro Matemática) | Reconocimiento de los factores común en las expresiones algebraicas | Aplicación de factor común y diferencia de cuadrados, página 26 | Factor común y trinomio cuadrado perfecto, página 18 | Aplicación de los diferentes trinomios cuando cambian los signos de un término, página 24 | Solución a cuestiones y problemas: ¿Cómo se representa el volumen de un cubo con una expresión algebraica? ¿Qué implica agregar un cubo?, ¿qué implica quitar un cubo? | |
b. Modelaje de sesión de clases[editar | editar código]
Clase presencial -Sesión 2
Paso 1: Exploración de conocimientos previos[editar | editar código]
Recorte cuadrados y rectángulos de papel para representar las expresiones que se presentan en la página 13 del libro Matemática.
Solicite a los estudiantes, a manera de juego, que construyan las expresiones que usted proponga; verifique que estas sean correctas y aproveche a corregir lo que sea necesario. En esta etapa del aprendizaje se trata de recordar o bien practicar un concepto para poder conectarlo con los siguientes. Con esta actividad se puede verificar que el estudiante utilice conocimientos previos como argumento de su razonamiento.
Paso 2: Nuevos conocimientos[editar | editar código]
El tema principal de esta sesión es la diferencia de cuadrados. Este tema se presta para la construcción geométrica de forma concreta, por lo que puede solicitar a los estudiantes que construyan un cuadrado de aproximadamente 10 cm de lado y le corten un cuadrado de 2 cm de lado en una de sus esquinas. Luego, deberán hacer el arreglo para construir un rectángulo que represente la expresión (x+a) (x-a), que, para este cuadrado queda así: (10+2) (10-2).
Con esto, justifique la expresión coloquial de: «… una vez sumando y otra, restando». En esta etapa es importante comprender que la factorización sirve como otra forma de representación algebraica de una misma situación: x2-a2=(x+a) (x-a). Para reconocer el algoritmo puede utilizar la página 20 del libro Matemática.
Paso 3: Integración-evaluación[editar | editar código]
Utilice la actividad de la página 26 para provocar reflexión sobre ¿qué sucede si a la expresión se le antepone un número? Esto permitirá la integración de conceptos. También puede utilizar la página 21 para practicar el algoritmo.
Agregue actividades de construcción de la factorización con cuadrados de diferentes medidas. Estas actividades pueden realizarse de forma colaborativa, en parejas —siempre con las medidas sanitarias pertinentes—, con el fin de discutir la temática propuesta. Este tipo de actividades permite evaluar el proceso de aprendizaje de los estudiantes.
Criterios de evaluación: según el currículo emergente para esta sesión se espera que el estudiante demuestre que «representa la factorización de diferencia de cuadrados en la geometría».
Conjunto de experiencias, planificadas o no, que tienen lugar en los centros educativos como posibilidad de aprendizaje del alumnado. Una perspectiva tradicional acentúa el carácter de plan (con elementos como objetivos, contenidos, metodología y evaluación), frente a un enfoque práctico que destaca las experiencias vividas en el proceso educativo.
Conjunto de sonidos articulados con que el hombre manifiesta lo que piensa o siente (DRAE). Facultad que sirve para establecer comunicación en un entorno social, se le considera como un instrumento del pensamiento para representar, categorizar y comprender la realidad, regular la conducta propia y de alguna manera, influir en los demás.
Evidencia de que la competencia se ha alcanzado por el o la estudiante.
Capacidad o disposición que ha desarrollado una persona para afrontar y dar solución a problemas de la vida cotidiana y a generar nuevos conocimientos. Es la capacidad para actuar de manera pertinente ante una situación compleja, movilizando de manera integrada los recursos necesarios para resolverla de modo adecuado.Tiene una doble dimensión: a) posesión de un conjunto de recursos o capacidades (cognitivos, de procedimientos y de actitudes), y b) capacidad para movilizarlos en una situación de acción.
En el continuo de coaching es el rol de ser muy directo y enseñar, mostrar, guiar, etc.
El género es un conjunto de valores, creencias e ideas sobre los comportamientos y actividades que en una determinada cultura son adecuados para las mujeres y los que son adecuados para los hombres, es decir, su identificación con la femineidad y con la masculinidad.
Proceso mecánico mediante el cual se aprende a representar palabras y oraciones con la claridad necesaria para que puedan ser leídas por alguien que tenga el mismo código lingüístico. La escritura es la representación gráfica de nuestro lenguaje.
Proceso en que los estudiantes participan en la evaluación de su propio proceso de aprendizaje y determinan de manera consciente qué pueden y qué no pueden hacer.
Proceso en que los estudiantes que participan en el proceso de aprendizaje evalúan el desempeño de otros estudiantes y reciben de ellos retroalimentación sobre su propio desempeño.
Proceso de evaluación de los estudiantes realizada por los docentes, padres y madres de familia u otros miembros de la comunidad.