14
| (No se muestran 9 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
| − | <span style="font-size:200%;;color: #ff0088">Resolución de problemas</span | + | {{#TwitterFBLike:right|like}}<span style="font-size:200%;;color: #ff0088">Resolución de problemas</span> |
[[Archivo:RESOLUCION_DE_PROBLEMAS.png |900px]] | [[Archivo:RESOLUCION_DE_PROBLEMAS.png |900px]] | ||
== <span style="color: #ff0088;">Presentación</span> == | == <span style="color: #ff0088;">Presentación</span> == | ||
| − | <span style="color: #ff0088;">La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del | + | <div style="float:right">__TOC__</div> |
| + | <span style="color: #ff0088;">La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del | ||
| + | área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.</span> | ||
| + | |||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| | | | ||
| Línea 9: | Línea 12: | ||
| | | | ||
<center>'''OBJETIVOS'''</center> | <center>'''OBJETIVOS'''</center> | ||
| − | * Analizar desde los procesos cognitivos los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del | + | * Analizar desde los procesos cognitivos, los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del Ciclo de Educación Básica del Nivel de Educación Media. |
* Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes. | * Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes. | ||
|} | |} | ||
|} | |} | ||
| + | |||
== <span style="color: #ff0088;">¿Cómo usar este documento?</span> == | == <span style="color: #ff0088;">¿Cómo usar este documento?</span> == | ||
| − | Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del | + | Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Ciclo de Educación Básica del Nivel de Educación Media. |
| − | de la prueba de | + | |
| − | estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país. | + | En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta la resolución de problemas, como una estrategia para adquirir las competencias matemáticas. A continuación, se presenta un ítem clonado de la prueba de Matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad de que el docente ubique el contenido evaluado dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza que apoya el desarrollo de la competencia matemática y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional. |
| + | |||
| + | En el apartado '''Análisis del error''', se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. | ||
| + | |||
| + | La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país. | ||
| + | |||
== <span style="color: #ff0088;">Resolución de problemas</span> == | == <span style="color: #ff0088;">Resolución de problemas</span> == | ||
| − | Un problema es un | + | Un problema es un desafío planteado para ser superado. El ser humano resuelve problemas de diferentes niveles de dificultad desde el más básico que es el de asegurar la cotidiana subsistencia, común a todos los seres vivos, hasta los más complejos planteados por la ciencia y la tecnología. |
| + | |||
| + | La importancia de la resolución de problemas es evidente; todo el progreso científico y tecnológico, el bienestar y hasta la supervivencia de la especie humana dependen de esta habilidad (Nieto, 2004). En el campo educativo es parte integral del currículo. En matemáticas no existe un método específico para resolver problemas; hay algunas orientaciones generales que conviene seguir: | ||
| + | |||
| + | (1) Leer el problema con todo cuidado para comprenderlo bien, es difícil resolver un problema del cual no se comprende el enunciado. | ||
| + | |||
| + | (2) Trazar un bosquejo del problema, conviene idear un problema específico que involucre una situación similar en la cual se conozcan todos los datos. | ||
| + | |||
| + | (3) Determinar cuáles son las cantidades conocidas y cuáles son las incógnitas. Usar una variable para representar una de las cantidades desconocidas en la ecuación a obtener. | ||
| + | |||
| + | (4) Escribir todos los datos numéricos conocidos y ordenarlos en una tabla. | ||
| + | |||
| + | (5) A partir de toda la información obtenida y si posee los conocimiento necesarios, entonces estará en capacidad de determinar las expresiones numéricas | ||
| + | que permitan obtener la solución del problema. | ||
| + | |||
| + | Por último es importante revisar los procedimientos realizados para verificar la respuesta; este último paso es importante porque la retroalimentación fortalece y desarrolla la habilidad para establecer las estrategias necesarias para la resolución de problemas. | ||
| + | |||
== <span style="color: #ff0088;">Análisis del ítem</span> == | == <span style="color: #ff0088;">Análisis del ítem</span> == | ||
| − | Al incluir ítems de | + | Al incluir ítems de resolución de problemas, se espera que el estudiante evidencie que establece un orden y estrategias para resolverlos. |
| + | |||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="25%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="25%" | ||
| | | | ||
| Línea 26: | Línea 52: | ||
| | | | ||
| − | Ana gana Q1,500.00 al mes. De esa cantidad, utiliza 15% en gasolina, 45% para el supermercado y un 20% para servicios básicos. Si en los últimos 6 meses | + | Ana gana Q1,500.00 al mes. De esa cantidad, utiliza 15% en gasolina, 45% para el supermercado y un 20% para servicios básicos. Si en los últimos 6 meses la gasolina ha subido en un 20%, ¿cuánto gastó en gasolina el último año? |
| − | ::a. | + | ::a. Q4 500<br /> |
| − | ::b. | + | ::b. Q3 150<br /> |
| − | ::<u>'''c. | + | ::<u>'''c. Q2 970'''</u><br /> |
| − | ::d. | + | ::d. Q4 320<br /> |
| + | |} | ||
|} | |} | ||
| + | <center>[[Archivo:Resoluciondeproblemas1.png |350px]]</center> | ||
| + | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="50%" | ||
| + | | <span style="color: #ffffff;"><center>Porcentaje de respuestas correctas en los ítems que evalúan resolución de problemas. '''29,6%'''</center></span> | ||
|} | |} | ||
| − | |||
La demanda cognitiva de este ítem, ubicada en Utilización, requiere del estudiante que '''aplique el conocimiento en situaciones específicas para resolver problemas.''' | La demanda cognitiva de este ítem, ubicada en Utilización, requiere del estudiante que '''aplique el conocimiento en situaciones específicas para resolver problemas.''' | ||
| + | |||
== <span style="color: #ff0088;">Análisis del error</span> == | == <span style="color: #ff0088;">Análisis del error</span> == | ||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| Línea 44: | Línea 74: | ||
# Operaciones básicas con números reales | # Operaciones básicas con números reales | ||
# Fracciones y sus operaciones | # Fracciones y sus operaciones | ||
| − | # Porcentajes | + | # Porcentajes. |
|} | |} | ||
|} | |} | ||
| Línea 50: | Línea 80: | ||
| | | | ||
| − | El ítem consiste en un problema escrito donde el gasto de gasolina en los primeros seis meses es: 0.15 ∙ | + | El ítem consiste en un problema escrito donde el gasto de gasolina en los primeros seis meses es: |
| + | |||
| + | <center><big>0.15 ∙ Q 1 500 ∙ 6 = Q 1 350.00</big></center> | ||
| + | |||
| + | y que, para los siguientes seis meses, el gasto con el correspondiente 20% de aumento es: | ||
| + | |||
| + | <center><big>(0.20 ∙ Q 1 350) + Q 1 350 = Q 1 620.00</big></center> | ||
| + | |||
| + | el total de gasto en un año es entonces: | ||
| + | |||
| + | <center><big>Q 2 970.00</big></center> | ||
|} | |} | ||
| + | |||
Los posibles errores cometidos por los estudiantes son los siguientes: | Los posibles errores cometidos por los estudiantes son los siguientes: | ||
| − | Si el estudiante eligió la opción… | + | |
| − | ::'''a.''' Determina que en los primeros 6 meses el gasto en gasolina es | + | Si el estudiante eligió la opción… |
| − | ::'''b.''' Interpreta incorrectamente que el gasto mensual en gasolina en la última mitad del año es del 20% del ingreso mensual que corresponde a Q 300.00, este valor lo multiplica por 6 meses y obtiene | + | ::'''a.''' Determina que en los primeros 6 meses el gasto en gasolina es Q 1 350.00 a razón de Q 225.00 por mes, para completar el análisis del año completo interpreta incorrectamente que cada mes la gasolina tiene un aumento del 35 % y resuelve que el gasto para los 6 meses restantes es Q 3 150.00 a razón de Q 525.00 por mes. Suma Q 1 350.00 + 3 150.00 y concluye que el gasto en gasolina anual es Q 4 500.00. |
| − | ::'''d.''' Obtiene que el gasto en gasolina en la primera mitad del año es de Q | + | ::'''b.''' Interpreta incorrectamente que el gasto mensual en gasolina en la última mitad del año es del 20 % del ingreso mensual que corresponde a Q 300.00, este valor lo multiplica por 6 meses y obtiene Q 1 800.00. Para completar el año determina que en los primeros 6 meses el gasto en gasolina es Q 1 350.00 a razón de Q 225.00 por mes, suma los valores totales y obtiene que el gasto en gasolina anual es Q 3 150.00. |
| + | ::'''d.''' Obtiene que el gasto en gasolina en la primera mitad del año es de Q 1 350.00, el limitado dominio del tema le hace suponer que como la otra mitad del año tiene 6 meses entonces el gasto también es de Q 1 350.00 mas el 20 % (Q 270.00 por mes) y obtiene que el gasto anual corresponde a Q 1 350 + Q 1 350 + 6( Q 270.00) que suman: Q 4 320.00. | ||
| + | |||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| | | | ||
| Línea 62: | Línea 105: | ||
| | | | ||
| − | En el CNB [[Malla curricular de Matemáticas - Tercer Grado#Escrito|competencia 3]] expresa que el estudiante “Utiliza los diferentes tipos de operaciones en el conjunto de números reales, aplicando sus propiedades y obteniendo resultados correctos. Para ello, se propone como indicador de logro: utilizar eficientemente los diferentes tipos de operaciones en el conjunto de números reales, aplicando sus propiedades y verificando que sus resultados son correctos. Los contenidos declarativos y procedimentales que permitirán desarrollar la competencia prevista son: Conjunto de números reales: orden operaciones y propiedades. Ejercitación en el cálculo mental y en las estimaciones. Aplicación de los elementos de los conjuntos y sus operaciones en la representación y resolución de problemas de la vida cotidiana. | + | En el CNB [[Malla curricular de Matemáticas - Tercer Grado#Escrito|competencia 3]] expresa que el estudiante “Utiliza los diferentes tipos de operaciones en el conjunto de números reales, aplicando sus propiedades y obteniendo resultados correctos. Para ello, se propone como indicador de logro: utilizar eficientemente los diferentes tipos de operaciones en el conjunto de números reales, aplicando sus propiedades y verificando que sus resultados son correctos. Los contenidos declarativos y procedimentales que permitirán desarrollar la competencia prevista son: Conjunto de números reales: orden operaciones y propiedades. Ejercitación en el cálculo mental y en las estimaciones. Aplicación de los elementos de los conjuntos y sus operaciones en la representación y resolución de problemas de la vida cotidiana.<ref>''Currículo Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado, 2010, p. 51''</ref> |
| − | <ref> | ||
|} | |} | ||
|} | |} | ||
| + | |||
== <span style="color: #ff0088;">Sugerencias de estrategias de aprendizaje</span> == | == <span style="color: #ff0088;">Sugerencias de estrategias de aprendizaje</span> == | ||
| − | + | # Para resolver problemas es importante que desarrolle creatividad en sus estudiantes. La creatividad es la habilidad de generar ideas nuevas y resolver problemas y desafíos de cualquier tipo. Algunas técnicas útiles son: | |
| − | + | #* Permita que el estudiante proponga distintas formas de resolver un problema. De esta manera no aprenderá de memoria las soluciones y entenderá qué está haciendo cuando se enfrente a los mismos. | |
| − | + | #* Divida el grupo de estudiantes en pequeños grupos de 3 o 4 personas y propóngales un problema de aritmética, algebra, ecuaciones lineales, problemas geométricos. Motive a que piensen la solución en equipo. Con este tipo de actividades logrará que los estudiantes imiten y propongan estrategias de resolución de problemas con menos temor. | |
| − | + | #* Hagan mapas mentales antes de resolver un problema. Esto les servirá para que los estudiantes logren identificar todas las partes importantes del problema y elaborar un plan para resolverlo. También ayuda que dibuje diagramas y/o figuras que representen el problema. | |
| − | + | # Enseñe y utilice alguna metodología para la resolución de problemas. La metodología de Pólya (Nieto, 2004) es una de las más fáciles y exitosas que existe. Esta consta de cuatro pasos: | |
| − | + | #* Comprensión del problema: Contestar a las preguntas: ¿Qué me piden? ¿Qué datos me dan? Con esta etapa se desea que el estudiante se detenga y reflexione sobre el problema sin resolverlo. La idea es que tenga bien claro qué le están pidiendo. | |
| − | + | #* Elaboración de un plan: Contestar a las preguntas: ¿Existe alguna expresión para representar mis datos? ¿Puedo construir un diagrama o una figura que represente mis datos? ¿He resuelto algún problema similar y en qué es diferente? ¿Puedo relacionar todos los datos? Con esta etapa se desea que el estudiante reflexione sobre lo que puede hacer y cómo lo va hacer. Obliga al estudiante a ir sobre conocimientos previos. | |
| − | + | #* Ejecución de un plan: Contestar a las preguntas: ¿Puedo ver que mis pasos son claros y correctos? Se desea que el estudiante evalúe si lo que ha propuesto de solución es claro. Algunas veces, las respuestas a la pregunta, nos llevará de regreso a la etapa anterior. | |
| − | + | #* Visión retrospectiva: Contestar a las preguntas: ¿Puedo obtener el resultado de otra forma? La idea es que el estudiante verifique de otra manera si su resultado es correcto. | |
| + | |||
== <span style="color: #ff0088;">Referencias</span> == | == <span style="color: #ff0088;">Referencias</span> == | ||
<references /> | <references /> | ||
| − | '''Documentos consultados''' | + | '''Documentos consultados''' |
| − | Cardenas, H. Curiel M. LLuis E. Peralta, F. Tavera C y Villa, E. (1975). Matemática a través de problemas. CECSA. Primera Edición. México. | + | # Cardenas, H. Curiel M. LLuis E. Peralta, F. Tavera C y Villa, E. (1975). ''Matemática a través de problemas''. CECSA. Primera Edición. México. |
| − | Nieto, S. J. (2004) Resolución de problemas matemáticos. Talleres de Formación Matemática. Maracaibo, Venezuela. Documento recuperado el 8 de junio de 2012. | + | # Nieto, S. J. (2004) [http://ommcolima.ucol.mx/guias/TallerdeResolucionproblemas.pdf ''Resolución de problemas matemáticos'']. Talleres de Formación Matemática. Maracaibo, Venezuela. Documento recuperado el 8 de junio de 2012. |
| − | Rodríguez, J. Caraballo, A. Cruz, T. Hernández O. (1997). Razonamiento Matemático | + | # Rodríguez, J. Caraballo, A. Cruz, T. Hernández O. (1997). ''Razonamiento Matemático: fundamentos y aplicaciones''. Thomson Editores SA. México. Pag. 131-152. |
| − | Matemáticas. 3º ESO. Sistemas de ecuaciones. Aplicaciones prácticas. Pág. 63 – 70. Documento recuperado el 8 de junio de 2012. | + | # ''Matemáticas. 3º ESO. [http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena4/3eso_quincena4.pdf "Sistemas de ecuaciones. Aplicaciones prácticas"]. Pág. 63 – 70. Documento recuperado el 8 de junio de 2012. |
| − | |||
[[Category:Matemáticas]] [[Category:Básico]] [[Categoría:Resultados de las evaluaciones]][[Category:Book:Serie_aprender_del_error]] | [[Category:Matemáticas]] [[Category:Básico]] [[Categoría:Resultados de las evaluaciones]][[Category:Book:Serie_aprender_del_error]] | ||
Revisión actual del 21:33 18 nov 2014
Resolución de problemas
Presentación[editar | editar código]
La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.
|
¿Cómo usar este documento?[editar | editar código]
Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Ciclo de Educación Básica del Nivel de Educación Media.
En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta la resolución de problemas, como una estrategia para adquirir las competencias matemáticas. A continuación, se presenta un ítem clonado de la prueba de Matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad de que el docente ubique el contenido evaluado dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza que apoya el desarrollo de la competencia matemática y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional.
En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida.
La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país.
Resolución de problemas[editar | editar código]
Un problema es un desafío planteado para ser superado. El ser humano resuelve problemas de diferentes niveles de dificultad desde el más básico que es el de asegurar la cotidiana subsistencia, común a todos los seres vivos, hasta los más complejos planteados por la ciencia y la tecnología.
La importancia de la resolución de problemas es evidente; todo el progreso científico y tecnológico, el bienestar y hasta la supervivencia de la especie humana dependen de esta habilidad (Nieto, 2004). En el campo educativo es parte integral del currículo. En matemáticas no existe un método específico para resolver problemas; hay algunas orientaciones generales que conviene seguir:
(1) Leer el problema con todo cuidado para comprenderlo bien, es difícil resolver un problema del cual no se comprende el enunciado.
(2) Trazar un bosquejo del problema, conviene idear un problema específico que involucre una situación similar en la cual se conozcan todos los datos.
(3) Determinar cuáles son las cantidades conocidas y cuáles son las incógnitas. Usar una variable para representar una de las cantidades desconocidas en la ecuación a obtener.
(4) Escribir todos los datos numéricos conocidos y ordenarlos en una tabla.
(5) A partir de toda la información obtenida y si posee los conocimiento necesarios, entonces estará en capacidad de determinar las expresiones numéricas que permitan obtener la solución del problema.
Por último es importante revisar los procedimientos realizados para verificar la respuesta; este último paso es importante porque la retroalimentación fortalece y desarrolla la habilidad para establecer las estrategias necesarias para la resolución de problemas.
Análisis del ítem[editar | editar código]
Al incluir ítems de resolución de problemas, se espera que el estudiante evidencie que establece un orden y estrategias para resolverlos.
|
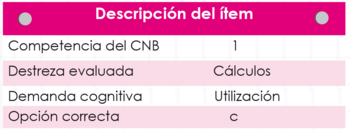
La demanda cognitiva de este ítem, ubicada en Utilización, requiere del estudiante que aplique el conocimiento en situaciones específicas para resolver problemas.
Análisis del error[editar | editar código]
|
|
El ítem consiste en un problema escrito donde el gasto de gasolina en los primeros seis meses es: y que, para los siguientes seis meses, el gasto con el correspondiente 20% de aumento es: el total de gasto en un año es entonces: |
Los posibles errores cometidos por los estudiantes son los siguientes:
Si el estudiante eligió la opción…
- a. Determina que en los primeros 6 meses el gasto en gasolina es Q 1 350.00 a razón de Q 225.00 por mes, para completar el análisis del año completo interpreta incorrectamente que cada mes la gasolina tiene un aumento del 35 % y resuelve que el gasto para los 6 meses restantes es Q 3 150.00 a razón de Q 525.00 por mes. Suma Q 1 350.00 + 3 150.00 y concluye que el gasto en gasolina anual es Q 4 500.00.
- b. Interpreta incorrectamente que el gasto mensual en gasolina en la última mitad del año es del 20 % del ingreso mensual que corresponde a Q 300.00, este valor lo multiplica por 6 meses y obtiene Q 1 800.00. Para completar el año determina que en los primeros 6 meses el gasto en gasolina es Q 1 350.00 a razón de Q 225.00 por mes, suma los valores totales y obtiene que el gasto en gasolina anual es Q 3 150.00.
- d. Obtiene que el gasto en gasolina en la primera mitad del año es de Q 1 350.00, el limitado dominio del tema le hace suponer que como la otra mitad del año tiene 6 meses entonces el gasto también es de Q 1 350.00 mas el 20 % (Q 270.00 por mes) y obtiene que el gasto anual corresponde a Q 1 350 + Q 1 350 + 6( Q 270.00) que suman: Q 4 320.00.
|
Sugerencias de estrategias de aprendizaje[editar | editar código]
- Para resolver problemas es importante que desarrolle creatividad en sus estudiantes. La creatividad es la habilidad de generar ideas nuevas y resolver problemas y desafíos de cualquier tipo. Algunas técnicas útiles son:
- Permita que el estudiante proponga distintas formas de resolver un problema. De esta manera no aprenderá de memoria las soluciones y entenderá qué está haciendo cuando se enfrente a los mismos.
- Divida el grupo de estudiantes en pequeños grupos de 3 o 4 personas y propóngales un problema de aritmética, algebra, ecuaciones lineales, problemas geométricos. Motive a que piensen la solución en equipo. Con este tipo de actividades logrará que los estudiantes imiten y propongan estrategias de resolución de problemas con menos temor.
- Hagan mapas mentales antes de resolver un problema. Esto les servirá para que los estudiantes logren identificar todas las partes importantes del problema y elaborar un plan para resolverlo. También ayuda que dibuje diagramas y/o figuras que representen el problema.
- Enseñe y utilice alguna metodología para la resolución de problemas. La metodología de Pólya (Nieto, 2004) es una de las más fáciles y exitosas que existe. Esta consta de cuatro pasos:
- Comprensión del problema: Contestar a las preguntas: ¿Qué me piden? ¿Qué datos me dan? Con esta etapa se desea que el estudiante se detenga y reflexione sobre el problema sin resolverlo. La idea es que tenga bien claro qué le están pidiendo.
- Elaboración de un plan: Contestar a las preguntas: ¿Existe alguna expresión para representar mis datos? ¿Puedo construir un diagrama o una figura que represente mis datos? ¿He resuelto algún problema similar y en qué es diferente? ¿Puedo relacionar todos los datos? Con esta etapa se desea que el estudiante reflexione sobre lo que puede hacer y cómo lo va hacer. Obliga al estudiante a ir sobre conocimientos previos.
- Ejecución de un plan: Contestar a las preguntas: ¿Puedo ver que mis pasos son claros y correctos? Se desea que el estudiante evalúe si lo que ha propuesto de solución es claro. Algunas veces, las respuestas a la pregunta, nos llevará de regreso a la etapa anterior.
- Visión retrospectiva: Contestar a las preguntas: ¿Puedo obtener el resultado de otra forma? La idea es que el estudiante verifique de otra manera si su resultado es correcto.
Referencias[editar | editar código]
- ↑ Currículo Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado, 2010, p. 51
Documentos consultados
- Cardenas, H. Curiel M. LLuis E. Peralta, F. Tavera C y Villa, E. (1975). Matemática a través de problemas. CECSA. Primera Edición. México.
- Nieto, S. J. (2004) Resolución de problemas matemáticos. Talleres de Formación Matemática. Maracaibo, Venezuela. Documento recuperado el 8 de junio de 2012.
- Rodríguez, J. Caraballo, A. Cruz, T. Hernández O. (1997). Razonamiento Matemático: fundamentos y aplicaciones. Thomson Editores SA. México. Pag. 131-152.
- Matemáticas. 3º ESO. "Sistemas de ecuaciones. Aplicaciones prácticas". Pág. 63 – 70. Documento recuperado el 8 de junio de 2012.
Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario
Habilidad, facilidad o arte para hacer algo bien hecho.
Capacidad o destreza para hacer algo bien o con facilidad.
Conjunto de experiencias, planificadas o no, que tienen lugar en los centros educativos como posibilidad de aprendizaje del alumnado. Una perspectiva tradicional acentúa el carácter de plan (con elementos como objetivos, contenidos, metodología y evaluación), frente a un enfoque práctico que destaca las experiencias vividas en el proceso educativo.
Término utilizado, a menudo, como un saber hacer. Se suele aceptar que, por orden creciente, en primer lugar estaría la habilidad, en segundo lugar la capacidad, y la competencia se situaría a un nivel superior e integrador. Capacidad es, en principio, la aptitud para hacer algo. Todo un conjunto de verbos en infinitivo expresan capacidades (analizar, comparar, clasificar, etc.), que se manifiestan a través de determinados contenidos (analizar algo, comparar cosas, clasificar objetos, etc.). Por eso son, en gran medida, transversales, susceptibles de ser empleadas con distintos contenidos. Una competencia moviliza diferentes capacidades y diferentes contenidos en una situación. La competencia es una capacidad compleja, distinta de un saber rutinario o de mera aplicación.
Un grupo de personas que trabajan hacia una meta común para el cual todos son mutuamente responsables.
