11
| Línea 50: | Línea 50: | ||
Los posibles errores cometidos por los estudiantes son los siguientes: | Los posibles errores cometidos por los estudiantes son los siguientes: | ||
Si el estudiante eligió la opción… | Si el estudiante eligió la opción… | ||
| − | a. no identifica una suma de fracciones con denominador común y opera como el producto de potencias de la misma base, empleando la ley de los | + | :'''a.''' no identifica una suma de fracciones con denominador común y opera como el producto de potencias de la misma base, empleando la ley de los exponentes enteros de la siguiente forma, en el numerador a∙a∙a = a3 y en el denominador b∙b∙b = b3. |
| − | exponentes enteros de la siguiente forma, en el numerador a∙a∙a = a3 y en el denominador b∙b∙b = b3. | + | :'''c.''' identifica una suma de fracciones equivalentes efectuando la suma correcta de los términos semejantes en el numerador: a+a+a = 3a, pero luego comete el error de repetir el mismo procedimiento en el denominador sumando los términos semejantes b+b+b = 3b, en lugar de expresar que el común denominador es b. |
| − | c. identifica una suma de fracciones equivalentes efectuando la suma correcta de los términos semejantes en el numerador: a+a+a = 3a, pero luego comete el error de repetir el mismo procedimiento en el denominador sumando los términos semejantes b+b+b = 3b, en lugar de expresar que el común denominador es b. | + | :'''d.''' identifica tres fracciones con denominador común, suma correctamente los términos semejantes en el numerador: a+a+a = 3a. Pero luego define de forma incorrecta que el denominador común de la expresión resultante es b3 y que es el resultado del producto b∙b∙b. |
| − | d. identifica tres fracciones con denominador común, suma correctamente los términos semejantes en el numerador: a+a+a = 3a. Pero luego define de | ||
| − | forma incorrecta que el denominador común de la expresión resultante es b3 y que es el resultado del producto b∙b∙b. | ||
{| style="border:2px solid #ff0088;border-radius: 4px;padding:8px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="65%" | {| style="border:2px solid #ff0088;border-radius: 4px;padding:8px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="65%" | ||
| | | | ||
| Línea 60: | Línea 58: | ||
En conclusión, los errores evidencian que los estudiantes no conocen el procedimiento para realizar suma de fracciones algebraicas. | En conclusión, los errores evidencian que los estudiantes no conocen el procedimiento para realizar suma de fracciones algebraicas. | ||
|} | |} | ||
| + | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| + | | | ||
| + | {| style="background:White;border:2px solid White;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="95%" | ||
| + | | | ||
| + | En el CNB la [[Malla curricular de Matemáticas - Tercer Grado#Escrito|competencia 1]] expresa que el estudiante “Produce patrones aritméticos, algebraicos y geométricos, aplicando propiedades y relaciones.”. Para ello, se propone como indicador de logro la aplicación de “factorización de polinomios al simplificar fracciones algebraicas y dividir polinomios.”. | ||
| + | Los contenidos declarativos y procedimentales que permitirán desarrollar la competencia prevista son los Polinomios y sus operaciones y propiedades, Productos Notables, Binomio de Newton, Triángulo de Pascal o de Tartaglia y Factorización. | ||
| + | <ref>Curriculum Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado. (2010), p. 49</ref> | ||
| + | |} | ||
| + | |} | ||
| + | == <span style="color: #ff0088;">Sugerencias de estrategias de aprendizaje</span> == | ||
| + | 1. Organice grupos de tres estudiantes. Al inicio de la semana asigne a cada grupo 2 ó 3 ejercicios que involucren: jerarquía de operaciones, simplificación, suma, resta, producto y división entre fracciones algebraicas. Se recomienda mezclar números enteros y fracciones. Indique que al final de la semana 4 o 5 grupos elegidos al azar deberán explicar los procedimientos de uno de los ejercicios ante el grupo en general. Esta exposición no debe ser mayor de 5 minutos y debe promover la participación de los estudiantes para que el aprendizaje sea activo. | ||
| + | Se recomiendan expresiones algebraicas de la forma:<br /> | ||
| + | [[Archivo:Fig5_FRACCIONES_ALGEBRAICAS.png|350px]]<br /> | ||
| + | 2. Prepare 2 ó 3 ejercicios por semana, establezca como máximo 15 minutos para resolverlas. Al finalizar el tiempo, dé a los estudiantes las respuestas correctas (sin el procedimiento) y que en los siguientes 5 minutos busquen los errores cometidos. Por último, en grupos de dos estudiantes que identifiquen sus errores y expliquen un procedimiento correcto. Se recomiendan expresiones algebraicas de la forma: | ||
| + | [[Archivo:Fig6_FRACCIONES_ALGEBRAICAS.png|350px]] | ||
| + | 3. Seleccione operaciones que involucren fracciones algebraicas y resuelva indicando de forma detallada cada uno de los procedimientos, de forma | ||
| + | intencionada cometa errores en la resolución que los estudiantes sean capaces de identificar. Reproduzca el material y oriente a sus estudiantes para que corrijan las operaciones sí consideran que los procedimientos son incorrectos. | ||
| + | Puede crear una historia que gire alrededor del problema donde se solicita la colaboración del grupo para que identifique los errores y sugiera los procedimientos correctos. | ||
| + | == <span style="color: #ff0088;">Referencias</span> == | ||
| + | <references /> | ||
| + | '''Documentos consultados'''<br /> | ||
| + | Aponte, G. (1998). Fundamento de Matemáticas Básicas. Primera Edición. Serie AWLI. Addison Wesley Longman. Mexico.487p.<br /> | ||
| + | Baldor, A. (1997). Álgebra. Publicaciones Cultural, S.A. de C.V. México D.F. 576p.<br /> | ||
| + | Astorga, A. y Rodríguez, J. (1984) Capítulo 1: El conjunto de los números reales. Instituto tecnológico de Costa Rica. Escuela de Matemática. Revista digital Matemática, educación e internet. Costa Rica. Recuperado el 8 de junio de 2012 http://www.cidse.itcr.ac.cr/cursos-linea/MATEGENERAL/t1-realesexpresionesalgebraicas/pdf/NumerosReales.pdf<br /> | ||
| + | Profesor en línea. Se puede utilizar citando la fuente www.profesorenlinea.cl - Querelle y Cia Ltda. Santiago- Chile. Recuperado el 8 | ||
| + | de junio de 2012 http://www.profesorenlinea.cl/matematica/Algebra_Fracciones.html | ||
Revisión del 23:15 27 ago 2014
Álgebra: fracciones algebraicas
Presentación[editar | editar código]
La Dirección General de Evaluación e Investigación Educativa,del Ministerio de Educación,encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas,del Nivel de Educación Media, del Ciclo de Educación Básica, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2009.
|
¿Cómo usar este documento?[editar | editar código]
Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Nivel de Educación Media, del Ciclo de Educación Básica. En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta el aprendizaje de las fracciones algebraicas. A continuación, se presenta un ítem clonado de la prueba de matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad de que el docente ubique el contenido dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza que apoya el desarrollo de la competencia matemática y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional. En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país.
Álgebra: fracciones algebraicas[editar | editar código]
Sí a y b son números reales y b ≠ 0 entonces a/b es una expresión fraccionaria donde a es el numerador y b es el denominador. Para sumar o restar fracciones algebraicas se emplea la siguiente propiedad de las fracciones:

Para aplicar estas propiedades es necesario que las fracciones tengan el mismo denominador. Sí suma o resta fracciones que no tengan el mismo denominador se deben reemplazar con fracciones equivalentes que tengan mínimo común denominador. Para hallar el mínimo común denominador se factoriza cada denominador en primos y luego se forma el producto de los diversos factores primos, utilizando el mayor exponente que aparezca en cada factor primo. El siguiente ejemplo ilustra el procedimiento para efectuar la adición:
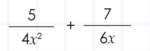

Análisis del ítem[editar | editar código]
Al incluir ítems de exponentes se espera que el estudiante evidencie que utiliza correctamente la simplificación de expresiones.


La demanda cognitiva de este ítem, ubicada en comprensión, requiere del estudiante recordar los procedimientos necesarios para simplificar fracciones algebraicas y aplicarlos correctamente.
Análisis del error[editar | editar código]
|

Los posibles errores cometidos por los estudiantes son los siguientes: Si el estudiante eligió la opción…
- a. no identifica una suma de fracciones con denominador común y opera como el producto de potencias de la misma base, empleando la ley de los exponentes enteros de la siguiente forma, en el numerador a∙a∙a = a3 y en el denominador b∙b∙b = b3.
- c. identifica una suma de fracciones equivalentes efectuando la suma correcta de los términos semejantes en el numerador: a+a+a = 3a, pero luego comete el error de repetir el mismo procedimiento en el denominador sumando los términos semejantes b+b+b = 3b, en lugar de expresar que el común denominador es b.
- d. identifica tres fracciones con denominador común, suma correctamente los términos semejantes en el numerador: a+a+a = 3a. Pero luego define de forma incorrecta que el denominador común de la expresión resultante es b3 y que es el resultado del producto b∙b∙b.
|
En conclusión, los errores evidencian que los estudiantes no conocen el procedimiento para realizar suma de fracciones algebraicas. |
|
Sugerencias de estrategias de aprendizaje[editar | editar código]
1. Organice grupos de tres estudiantes. Al inicio de la semana asigne a cada grupo 2 ó 3 ejercicios que involucren: jerarquía de operaciones, simplificación, suma, resta, producto y división entre fracciones algebraicas. Se recomienda mezclar números enteros y fracciones. Indique que al final de la semana 4 o 5 grupos elegidos al azar deberán explicar los procedimientos de uno de los ejercicios ante el grupo en general. Esta exposición no debe ser mayor de 5 minutos y debe promover la participación de los estudiantes para que el aprendizaje sea activo.
Se recomiendan expresiones algebraicas de la forma:

2. Prepare 2 ó 3 ejercicios por semana, establezca como máximo 15 minutos para resolverlas. Al finalizar el tiempo, dé a los estudiantes las respuestas correctas (sin el procedimiento) y que en los siguientes 5 minutos busquen los errores cometidos. Por último, en grupos de dos estudiantes que identifiquen sus errores y expliquen un procedimiento correcto. Se recomiendan expresiones algebraicas de la forma:
![]() 3. Seleccione operaciones que involucren fracciones algebraicas y resuelva indicando de forma detallada cada uno de los procedimientos, de forma
intencionada cometa errores en la resolución que los estudiantes sean capaces de identificar. Reproduzca el material y oriente a sus estudiantes para que corrijan las operaciones sí consideran que los procedimientos son incorrectos.
Puede crear una historia que gire alrededor del problema donde se solicita la colaboración del grupo para que identifique los errores y sugiera los procedimientos correctos.
3. Seleccione operaciones que involucren fracciones algebraicas y resuelva indicando de forma detallada cada uno de los procedimientos, de forma
intencionada cometa errores en la resolución que los estudiantes sean capaces de identificar. Reproduzca el material y oriente a sus estudiantes para que corrijan las operaciones sí consideran que los procedimientos son incorrectos.
Puede crear una historia que gire alrededor del problema donde se solicita la colaboración del grupo para que identifique los errores y sugiera los procedimientos correctos.
Referencias[editar | editar código]
- ↑ Curriculum Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado. (2010), p. 49
Documentos consultados
Aponte, G. (1998). Fundamento de Matemáticas Básicas. Primera Edición. Serie AWLI. Addison Wesley Longman. Mexico.487p.
Baldor, A. (1997). Álgebra. Publicaciones Cultural, S.A. de C.V. México D.F. 576p.
Astorga, A. y Rodríguez, J. (1984) Capítulo 1: El conjunto de los números reales. Instituto tecnológico de Costa Rica. Escuela de Matemática. Revista digital Matemática, educación e internet. Costa Rica. Recuperado el 8 de junio de 2012 http://www.cidse.itcr.ac.cr/cursos-linea/MATEGENERAL/t1-realesexpresionesalgebraicas/pdf/NumerosReales.pdf
Profesor en línea. Se puede utilizar citando la fuente www.profesorenlinea.cl - Querelle y Cia Ltda. Santiago- Chile. Recuperado el 8
de junio de 2012 http://www.profesorenlinea.cl/matematica/Algebra_Fracciones.html
Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario
Habilidad, facilidad o arte para hacer algo bien hecho.
Conjunto de acciones (formas de actuar o de resolver tareas), con un orden, plan o pasos, para conseguir un determinado fin o meta. Se trata de saber hacer cosas, aplicar o actuar de manera ordenada para solucionar problemas, satisfacer propósitos o conseguir objetivos. Forman los contenidos procedimentales.
