Tema 4. Números racionales II

Inicio

Indicadores de logro

1. Multiplica y divide fracciones propias e impropias.
2. Resuelve ecuaciones de primer grado que incluyan fracciones.

Todas las actividades de este tema son para que usted realice. Si tiene oportunidad reúnase con otros docentes y compartan. Se recomienda aplicarlas con sus estudiantes del ciclo básico.

1. Lea y resuelva.

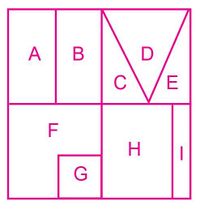
La Figura 1 muestra una caja vista desde arriba que está dividida en 4 cuadrantes y varios compartimientos de distinto tamaño.

• Tome una hoja de papel, corte para conseguir un cuadrado.
• Divida el cuadrado de papel en 4 cuadrantes.
• Realice dobleces tal como se indica en la Figura 1, para establecer los compartimientos numerados.
• Emplee su conocimiento para asociar a cada porción de la caja, identificada con una letra, una fracción respectiva.
• Sume las fracciones. Demuestre que el resultado obtenido es 1.

Figura

2. Lea, resuelva y exponga.

La abuelita de Carolina le prepara un pastel de cumpleaños. Utiliza 2 ¼ libras de manzanas, 1/2 libra de harina y otros ingredientes que, en la balanza, marcan 3/8 de libra. Para hornearla tiene un molde que dice 3 ½ libras. Ella está un poco indecisa entre prepararla con esos ingredientes (los de su receta favorita) o en suprimir algunos. ¿Cómo la ayudaría a tomar una decisión?

• Plantee una estrategia para ayudar a la abuelita de Carolina. Compártala.
• Elija la que considera más aceptable. ¿Es posible preparar el pastel para Carolina?

Uno de los más conocidos experimentos de Pasteur consistió en lo siguiente: se pusieron a su disposición 50 ovejas, la mitad de las cuales fueron vacunadas. Luego todas las ovejas recibieron una dosis de bacilos de peste de ovejas, suficientes para provocar la muerte.

Cuando llegó el día de comprobar los resultados, la mitad de las ovejas, las que fueron vacunadas, estaban sanas; los 3/50 de las ovejas estaban a punto de morir y el resto había muerto ya. ¿Qué fracción del número inicial de ovejas había muerto?

• Forme un grupo de trabajo y proponga procedimientos para hallar la solución a la situación.
• Elabore un cartel con la estrategia utilizada.
• Exponga con sus compañeros cómo llegaron a la solución del enunciado.

Desarrollo

Nuevos aprendizajes

Multiplicación de números racionales (fracciones): Para multiplicar dos números racionales, multiplica los numeradores y los denominadores.

División de números racionales (fracciones): Para dividir entre un número racional, se multiplica por su inverso.

• Copie y complete en el cuaderno la Tabla 1.
• Simplifique las soluciones hasta fracciones irreducibles.
• Identifique la opción correcta.

Tabla 1

Ej. 2/3 ÷ 5/6=2/3*6/5=4/5				Ej. 7/4*3/7=3/4
[math]\displaystyle{ \frac {7}{3}\div\frac {2}{4} }[/math]	[math]\displaystyle{ \frac {28}{6} }[/math]	[math]\displaystyle{ \frac {14}{3} }[/math]	[math]\displaystyle{ \frac {14}{12} }[/math]	[math]\displaystyle{ 6/5*4/3=? }[/math]	[math]\displaystyle{ 5/8 }[/math]	[math]\displaystyle{ 8/5 }[/math]	[math]\displaystyle{ 1 3/8 }[/math]
[math]\displaystyle{ \frac {8}{5}\div\frac {5}{2} }[/math]	[math]\displaystyle{ \frac {15}{16} }[/math]	[math]\displaystyle{ \frac {24}{10} }[/math]	[math]\displaystyle{ \frac {15}{16} }[/math]	[math]\displaystyle{ 2 ½*7/9=? }[/math]	[math]\displaystyle{ 5/3 }[/math]	[math]\displaystyle{ 7/6 }[/math]	[math]\displaystyle{ 35/18 }[/math]

Solución de ecuaciones con racionales

Para solucionar ecuaciones con racionales se determina qué operación (suma, resta, multiplicación o división) se debe aplicar a la variable. Se utilizan operaciones inversas, propiedad del inverso aditivo o propiedad del inverso multiplicativo.

Para resolver una ecuación como: x-[math]\displaystyle{ \frac {4}{5}=\frac {3}{10} }[/math] x[math]\displaystyle{ \frac {4}{5}-\frac {4}{5}=\frac {3}{10}+\frac {4}{5} }[/math]

Propiedad de la igualdad de la suma x=[math]\displaystyle{ \frac {3}{10}+\frac {8}{10}; x=\frac {11}{10}= 1\frac {1}{10} }[/math]

Se verifica y sustituye x con \frac {11}{10}</math>

[math]\displaystyle{ (\frac {11}{10}) }[/math]