Tema 3. Polígonos

Inicio

Indicadores de logro

1. Nombra e ilustra polígonos regulares e irregulares.
2. Resuelve problemas asociados a los ángulos internos de un polígono.
3. Utiliza información de los polígonos regulares para determinar perímetros y áreas.

Todas las actividades de este tema son para que usted realice. Si tiene oportunidad reúnase con otros docentes y compartan. Se recomienda aplicarlas con sus estudiantes del ciclo básico.

1. Lea y resuelva.

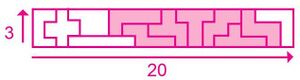
Las formas de la Figura 1 se llaman pentóminos, porque son 12 formas y cada una contiene cinco cuadros.

• Trace las formas de la figura 1 en una hoja milimetrada (1 cm) o cuadricula y recorte los pentóminos.
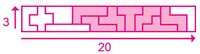
• Forme la figura 2, de tres cuadros de alto y 20 cuadros de largo, con los 12 pentóminos que recorte, encuentre el perímetro de la figura.
• Utilice los 12 pentóminos para forma una letra “L”, y encuentre el perímetro.
• Forme dos figuras más y calcule el perímetro, comparta sus hallazgos.

Figura 1

Figura 2

2. Lea, resuelva y exponga los resultados.

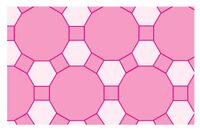
Cuando se cubre una superficie con un patrón de formas planas de manera que no se superponen ni hay espacios vacíos se dice que es una teselación.

En la figura 3 muestra una teselación 4*8*8, llamada así, porque cada vértice es la unión de un cuadrado (4 lados) y dos octágonos (8 lados).

Figura 2

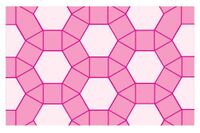
Marcos es alcalde de su municipio. El salón comunal necesita cambio de piso. Marcos se ha decidió por dos modelos de piso (figura 4), pero le surge una duda: ¿Cómo se forman tan maravillosas figuras?

• Escriba un mensaje a Marcos explicándole cómo se forman y el número para cada diseño.

• 
• 

Figura 4

Desarrollo

Nuevos aprendizajes

Un polígono es una figura plana formada por tres o más segmentos que se intersecan solo en los puntos extremos de manera que solo dos segmentos se tocan en cada punto extremo. Los polígonos reciben un nombre de acuerdo con el número de lados. En un polígono regular, todos los lados y ángulos miden lo mismo, cuando un polígono no es regular se llama irregular.

• Observe los polinomios de la figura 5.
  Clasifíquelos como regular o irregular según el número de lados. Explique sus hallazgos.

• 
• 
• 
• 

Figura 5

Cuadrilátero

Un cuadrilátero es un polígono con cuatro lados. La suma de las medidas de los ángulos de un cuadrilátero es igual a 360°.

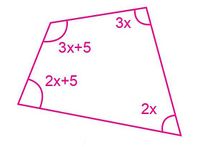
• Calcule x y sustituya para hallar los ángulos del cuadrilátero en la figura 6:
  2x + (2x +5) + (3x + 5) + 3x = 260; 10x + 10 = 360; x =35°

• Calcule el valor numérico de los ángulos del cuadrilátero si están representados por: x; (x + 6); (2x-2); (x +1)

Figura 6

Área de polígono

En un polígono regular sus lados son congruentes. Un polígono se puede descomponer en tantos triángulos isósceles como lados tenga. La altura de cada triángulo isósceles la consideramos como el segmento de recta perpendicular, trazado desde el punto O al lado del polígono y recibe el nombre de apotema. Entonces la región plana limitada por un polígono regular de n lados, es la unión de la n regiones triangulares en que se puede descomponer, entonces eso nos permite calcular el área de un polígono de la siguiente manera:

Área_polígono = Área_triángulo*n_triángulos; otra forma para hallar el área del polígono será:

[math]\displaystyle{ \frac {Perimetro \lt sub\gt polígono\lt /sub\gt =* apotema}{2}=A=\lt math\gt \frac {P * a}{2} }[/math]</math>

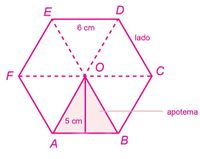
• Calcule el área del hexágono de la figura 6, de la siguiente manera:

[math]\displaystyle{ Área \lt sub\gt hexágono\lt /sub\gt \frac {6 * 6 * 5}{2}=\frac {180}{2}=90cm^2; }[/math]

• Calcule si ahora el lado del hexágono mide 10 cm y la apotema mide de 8 cm. Compare su resultado.

Cierre

Ejercicios del tema

Nivel: Conocimiento y recuerdo

1. Identifique y examine las situaciones. Misael recortó los polígonos que se muestran en la figura 8, pero tiene dudas sobre los polígonos que observa.

• Identifique los polígonos y explique las diferencias y las similitudes entre ellos.

2. Plantee una estrategia para ayudar en la tarea y compártala.

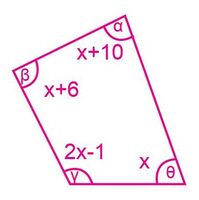
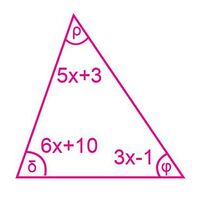
Jocabed tiene como tarea calcular los ángulos internos de los polígonos que se muestran en la figura 9.

• Encuentre x para cada polígono de la figura 9.
  Luego sustituya para calcular los ángulos de cada uno.

• 
• 

Figura 9

3. Calcule cuánto material necesita para hacerlas.
Explique su estrategia.

Noé tiene a su cargo hacer la figura 10, para la exposición matemática de mañana. Cuánto material necesita comprar, si él sabe que en la clase de matemáticas hay 15 estudiantes.

200px

Figura 10

Destrezas fonológica que consiste en juntar fonemas o sílabas para formar una palabra.