Tema 3. Funciones
Inicio
Indicadores de logro
- Identifica el dominio y contradominio de una función.
- Reconoce la función constante e identidad.
1. Analice las siguientes situaciones y resuelva en el cuaderno.
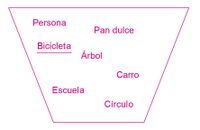
- Relacione cada elemento del conjunto A con un elemento del conjunto B. Vea la figura 1.
No escriba sus resultados sobre el libro. Únicamente exprese en forma verbal las distintas relaciones que encuentre entre los elementos. Por ejemplo: “a cada bicicleta le corresponden 'un par de llantas”.
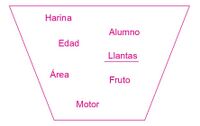
2. Calcule los valores de salida del conjunto S.
- Para relacionar el conjunto de ingreso I y el conjunto de salida S, se utiliza una condición, tal como se muestra en la figura 2.
Una función es una regla que produce una correspondencia entre los elementos de dos conjuntos. En la primera situación, relacionó los elementos por la experiencia personal y concluyó que a cada persona le corresponde una edad, a cada carro le corresponde un motor, a cada círculo le corresponde un área, etc. En la segunda situación, la experiencia fue sustituida por una condición matemática que generó los siguientes números en el conjunto S: -3, -4, -17, 43 o 211, entre otros valores.
Desarrollo
Nuevos aprendizajes
Una relación es un conjunto de parejas ordenadas (x, y). Los valores x forman el dominio y los valores y el rango de la relación. Una función es una relación donde a cada valor x le corresponde un solo valor y.
1. Analice las diferentes formas de describir una relación.
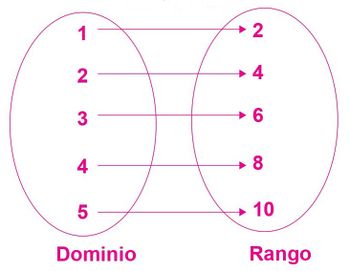
Enunciado:[math]\displaystyle{ \to }[/math] Cada número entero del 1 al 5 se asocia con su doble.
| Dominio | x | 1 | 2 | 3 | 4 | 5 |
| Rango | y | 2 | 4 | 6 | 8 | 10 |
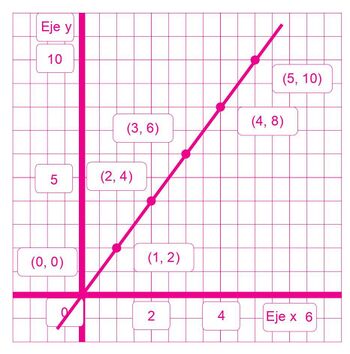
Parejas ordenadas:
{(1, 2), (2,4), (3 ,6), (4, 8), (5, 10)}
Responda al siguiente cuestionamiento:
¿Cuál de las siguientes relaciones son funciones?
- a) {(0, 2), (1, 3), (0 ,4), (3, 5)}
- b) {(-1, 2), (- 2, 3), (- 4 ,5), (- 5, 5)}
- c) {(-1, 8), (0, 8), (1 ,8)}
La respuesta a las preguntas anteriores son las siguientes:
- a) No es una función, esto debido a que al número 0 se le asocian dos valores de y.
- b) Si es función, se evidencia que a cada valor de x se lo asocia un solo valor de y.
- c) Si es función, observe que cada valor de x se le asocia un valor de y, en este caso se llama: función constante.
- Represente cada una de las situaciones anteriores en un plano cartesiano.
¿Qué más necesito saber?
El símbolo f (x) representa al número real en el rango, también llamado: recorrido, imagen o contradominio. La notación f: A → B, se lee: “f de A en B” y se interpreta como: la función f que va del conjunto A (dominio) al conjunto B, (contradominio).
1. Analice las siguientes situaciones.
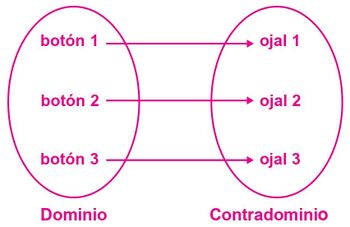
Los botones y ojales de una camisa.
A cada botón le corresponde un solo ojal de una camisa. Dos botones distintos no pueden ir en un mismo ojal. Esta función es uno a uno y sobreyectiva, por lo que recibe el nombre de biunívoca y se puede representar de la siguiente forma: f: A → B, donde A son botones y ojales son B.
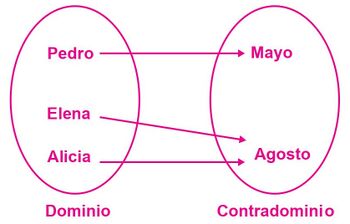
La relación f: A → B, donde a cada persona del conjunto A se le asocia un mes de nacimiento B, es una función porque ninguna persona pudo haber nacido en dos fechas distintas. No es uno a uno porque muchas personas poseen el mismo mes de nacimiento. Este tipo de función es sobreyectiva o suprayectiva porque todo elemento del dominio está asociado con un elemento del contradominio.
Revise el siguiente enlace para repasar las funciones:
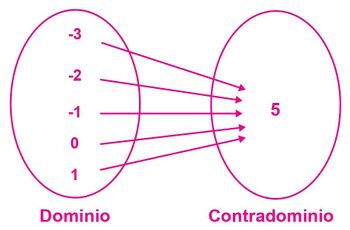
Función constante. Todos los valores del dominio se asocian a un único valor del contradominio.
La relación se define: [math]\displaystyle{ f: R \to {5} }[/math] y su función es [math]\displaystyle{ y = f (x) = 5 }[/math].
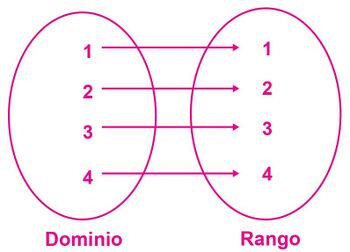
Función identidad. A cada valor del dominio le corresponde el mismo valor en el contradominio.
La relación se define: [math]\displaystyle{ f: R \to R }[/math] y su función es [math]\displaystyle{ y = f (x) = x }[/math].
Cierre
Ejercicios del tema
Nivel: Comprensión
1. Lea y analice las siguientes situaciones.
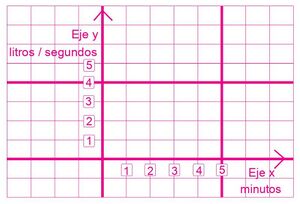
Durante una intensa lluvia, Roberto mide el flujo de agua en litros por segundo en el drenaje de la comunidad y verifica que se mantiene constante durante cinco minutos.
- Observe la gráfica de esta situación.
2. Responda.
- ¿Qué valores tiene el dominio?
- ¿Qué valores tiene el rango o contradominio?
- ¿Es una función uno a uno o sobre?
Esta es una función constante porque relaciona los elementos del conjunto dominio: {1, 2, 3, 4, 5}, con un único elemento del conjunto contradominio que es el flujo de 4 l/s. La relación se expresa como y = f (x) = 4.
3. Lea y resuelva.
Antonio viaja en motocicleta sobre una carretera plana y en línea recta, los valores de la velocidad en kilómetros por hora durante un tiempo de ocho minutos se registran en la siguiente tabla.
| Tiempo | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Velocidad | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
- ¿Qué valores tiene el dominio?
- ¿Qué valores tiene el rango o contradominio?
- Trace la gráfica de la función en papel milimetrado.
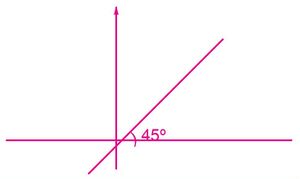
4. Trace la gráfica en el plano cartesiano de una función identidad y verifique que la recta está inclinada 45° con respecto del eje x.
- Utilice papel milimetrado y transportador.
- Complete la siguiente tabla.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y |
5. Responda: ¿Es una función uno a uno o sobreyectiva?
La función es: y=x; cumple condiciones biyectiva y sobreyectiva.