Tema 4. Números racionales II

Inicio

Indicadores de logro

1. Multiplica y divide fracciones propias e impropias.
2. Resuelve ecuaciones de primer grado que incluyan fracciones.

Todas las actividades de este tema son para que usted realice. Si tiene oportunidad reúnase con otros docentes y compartan. Se recomienda aplicarlas con sus estudiantes del ciclo básico.

1. Lea y resuelva.

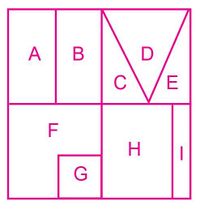
La Figura 1 muestra una caja vista desde arriba que está dividida en 4 cuadrantes y varios compartimientos de distinto tamaño.

• Tome una hoja de papel, corte para conseguir un cuadrado.
• Divida el cuadrado de papel en 4 cuadrantes.
• Realice dobleces tal como se indica en la Figura 1, para establecer los compartimientos numerados.
• Emplee su conocimiento para asociar a cada porción de la caja, identificada con una letra, una fracción respectiva.
• Sume las fracciones. Demuestre que el resultado obtenido es 1.

Figura

2. Lea, resuelva y exponga.

La abuelita de Carolina le prepara un pastel de cumpleaños. Utiliza 2 ¼ libras de manzanas, 1/2 libra de harina y otros ingredientes que, en la balanza, marcan 3/8 de libra. Para hornearla tiene un molde que dice 3 ½ libras. Ella está un poco indecisa entre prepararla con esos ingredientes (los de su receta favorita) o en suprimir algunos. ¿Cómo la ayudaría a tomar una decisión?

• Plantee una estrategia para ayudar a la abuelita de Carolina. Compártala.
• Elija la que considera más aceptable. ¿Es posible preparar el pastel para Carolina?

Uno de los más conocidos experimentos de Pasteur consistió en lo siguiente: se pusieron a su disposición 50 ovejas, la mitad de las cuales fueron vacunadas. Luego todas las ovejas recibieron una dosis de bacilos de peste de ovejas, suficientes para provocar la muerte.

Cuando llegó el día de comprobar los resultados, la mitad de las ovejas, las que fueron vacunadas, estaban sanas; los 3/50 de las ovejas estaban a punto de morir y el resto había muerto ya. ¿Qué fracción del número inicial de ovejas había muerto?

• Forme un grupo de trabajo y proponga procedimientos para hallar la solución a la situación.
• Elabore un cartel con la estrategia utilizada.
• Exponga con sus compañeros cómo llegaron a la solución del enunciado.

Desarrollo

Nuevos aprendizajes

Multiplicación de números racionales (fracciones): Para multiplicar dos números racionales, multiplica los numeradores y los denominadores.

División de números racionales (fracciones): Para dividir entre un número racional, se multiplica por su inverso.

• Copie y complete en el cuaderno la Tabla 1.
• Simplifique las soluciones hasta fracciones irreducibles.
• Identifique la opción correcta.

Tabla 1

Ej. 2/3 ÷ 5/6=2/3*6/5=4/5				Ej. 7/4*3/7=3/4
[math]\displaystyle{ \frac {7}{3}\div\frac {2}{4} }[/math]	[math]\displaystyle{ \frac {28}{6} }[/math]	[math]\displaystyle{ \frac {14}{3} }[/math]	[math]\displaystyle{ \frac {14}{12} }[/math]	[math]\displaystyle{ 6/5*4/3=? }[/math]	[math]\displaystyle{ 5/8 }[/math]	[math]\displaystyle{ 8/5 }[/math]	[math]\displaystyle{ 1 3/8 }[/math]
[math]\displaystyle{ \frac {8}{5}\div\frac {5}{2} }[/math]	[math]\displaystyle{ \frac {15}{16} }[/math]	[math]\displaystyle{ \frac {24}{10} }[/math]	[math]\displaystyle{ \frac {15}{16} }[/math]	[math]\displaystyle{ 2 1/2*7/9=? }[/math]	[math]\displaystyle{ 5/3 }[/math]	[math]\displaystyle{ 7/6 }[/math]	[math]\displaystyle{ 35/18 }[/math]

Solución de ecuaciones con racionales

Para solucionar ecuaciones con racionales se determina qué operación (suma, resta, multiplicación o división) se debe aplicar a la variable. Se utilizan operaciones inversas, propiedad del inverso aditivo o propiedad del inverso multiplicativo.

Para resolver una ecuación como: x-[math]\displaystyle{ \frac {4}{5}=\frac {3}{10} }[/math] x[math]\displaystyle{ \frac {4}{5}-\frac {4}{5}=\frac {3}{10}+\frac {4}{5} }[/math]

Propiedad de la igualdad de la suma x=[math]\displaystyle{ \frac {3}{10}+\frac {8}{10}; x=\frac {11}{10}= 1\frac {1}{10} }[/math]

Se verifica y sustituye x con [math]\displaystyle{ \frac {11}{10} }[/math]

[math]\displaystyle{ (\frac {11}{10})-\frac {4}{5}=\frac {3}{10} }[/math]

[math]\displaystyle{ \frac {11}{10}-\frac {8}{10}=\frac {3}{10} }[/math]

[math]\displaystyle{ \frac {3}{10}=\frac {3}{10} }[/math]

Para resolver una ecuación como: [math]\displaystyle{ \frac {3}{4}x=\frac{5}{8} }[/math]

[math]\displaystyle{ (\frac {4}{3})*\frac {3}{4}x=\frac{5}{8}*(\frac {4}{3}) }[/math]

Se multiplica ambos lados por el recíproco de 3/4

[math]\displaystyle{ 1*x=\frac {20}{24}; x=\frac{5}{6} }[/math]

Se verifica y sustituye x con [math]\displaystyle{ \frac {5}{6} }[/math]

[math]\displaystyle{ \frac {3}{4} (\frac {5}{6})=\frac {5}{8} }[/math]

[math]\displaystyle{ \frac {15}{24}=\frac {5}{8} }[/math]

[math]\displaystyle{ \frac {5}{8}=\frac {5}{8} }[/math]

Copie y resuelva en el cuaderno. Verifique sus soluciones como en el ejemplo.

1)[math]\displaystyle{ \frac {3}{7}=h+\frac {4}{5} }[/math]

2)[math]\displaystyle{ -\frac {6}{5}=-\frac {2}{3}+w }[/math]

3)[math]\displaystyle{ 4f=\frac {3}{4} }[/math]

Cierre

Ejercicios del tema

Nivel: Conocimiento y recuerdo

1. Identifique y examine las situaciones.

Un terreno rectangular tiene un área de [math]\displaystyle{ \frac {1}{2} }[/math] [math]\displaystyle{ m^2 }[/math].

• Si la base mide [math]\displaystyle{ \frac {1}{4} }[/math]m, ¿se puede calcular cuánto mide la altura? ¿Y si la base mide 4m?

• Y si la base mide [math]\displaystyle{ \frac {1}{5} }[/math]m, calcule ¿cuánto mide el área sabiendo que la altura es de [math]\displaystyle{ \frac {2}{3} }[/math] m?

Erick tiene un terreno rectangular y lo divide en 15 partes iguales. Él planifica sembrar zanahorias en una sección del terreno que tiene [math]\displaystyle{ \frac {2}{3} }[/math] de largo [math]\displaystyle{ \frac {4}{5} }[/math] de ancho.

• Dibuje el terreno completo de Erick.
• Encuentre el área de siembra de zanahorias y coloréelo con crayones.
• Responda: ¿qué fracción del terreno queda vacío? Explique.

Q es la cantidad de dinero que le queda en la cuenta de ahorro a Felipe. Luego de realizar operaciones bancarias, la expresión [math]\displaystyle{ \frac {12}{5} \frac {2}{3} Q=3 }[/math] representa la cantidad de dinero en la cuenta. ¿Qué fracción de dinero queda?

• Encuentre la solución y verifique el resultado.
• Interprete y explique su hallazgo.

Nivel: Comprensión. Organiza y relaciona la información

2. Lea y resuelva.

Un robot se desplaza por una recta numérica con pasos regulares que miden 1/5 de la unidad.

Por ejemplo, si el robot está parado en 0 y da 3 pasos estará parado en 3/5. Si da 2 pasos más, estará parado en el 1.

Si el robot está parado en el 5/4, ¿será cierto que después de avanzar 17 pasos todavía no llegará a 4?

• ¿Puede decir qué número de pasos dio cuando esté parado en 4, si sale de 4 1/2?
• Explique sus soluciones.

Julio y Claudia son hermanos. Juntos compraron un terreno. Julio se quedó con 4/9 y Claudia con 5/9 del terreno. Ana, la esposa de Julio, heredó 2/3 de un terreno del mismo tamaño que el de Julio y Claudia.

• Demuestre quién tiene el terreno de mayor tamaño por medio de las fracciones de Ana y Julio, si el terreno es de 270 [math]\displaystyle{ m^2 }[/math].

Nivel: Análisis

3. Ordene los datos y plantee estrategias.

De las cuatro docenas de las golosinas que le regalaron a Pablo, 3/8 son de chocolate, 2/5 del resto son de fruta y las demás golosinas, son de dulce de leche.

4. Calcule.

• ¿Cuántas golosinas de chocolate le regalaron?
• ¿Cuántos de fruta?
• ¿Qué parte del total son de chocolate?
• ¿Qué parte del total son de fruta?
• ¿Qué parte del total son de dulce de leche?
• ¿Cuántas son de dulce de leche?

Tabla 2

Cantidad de invitados	[math]\displaystyle{ 5 }[/math]		[math]\displaystyle{ 3 }[/math]
Cantidad de helado necesaria (en kg)		[math]\displaystyle{ 1\frac {1}{2} }[/math]	[math]\displaystyle{ 3\frac {3}{4} }[/math]

Se debe comprar la suficiente cantidad de helado para dar 1/4 kg a cada invitado en una fiesta. Complete la Tabla 2 en la que se relaciona la cantidad de invitados con la cantidad de kilogramos de helado necesaria, si se quiere dar siempre 1/4 kg a cada invitado.

Nivel: Utilización

5. Utilice la información para resolver los planteamientos y calcule.

Valeria se comió 1/5 de los jocotes de una caja y Felipe ½ de la misma.

• ¿Qué fracción se comieron entre los dos, si quedaron 12 jocotes en la caja?
• ¿Cuántos jocotes tenía la caja?

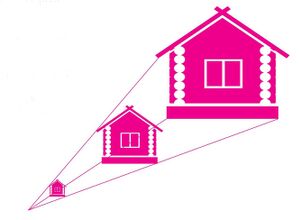
Quetzalí es una pintora de perspectiva y a la vez disfruta de la matemática. La Figura 2 muestra uno de sus trabajos donde cada vivienda tiene una expresión algebraica asociada. Según Quetzalí: la mayor es x, la vivienda del medio es la tercera parte de x y la menor es la cuarta parte de x. Si todo en conjunto suma dos veces x disminuido en 17.

• Escriba la ecuación para esta situación.
• Encuentre el valor de x que expresa el área de la vivienda mayor.

Figura 2

Resultados a los ejercicios del tema

Compruebe sus resultados a los ejercicios del tema con esta tabla.

Respuestas de la fase de inicio

1. Identifique [math]\displaystyle{ A=1/8; B=1/8; C=1/16; D=2/16; E= 1/16; F= 3/16; G=1/16; H=3/16; I=1/16. }[/math]

La suma es 1.

2. Sume:[math]\displaystyle{ 2\frac{1}{4}+\frac{1}{2}+\frac{3}{8}=3\frac{1}{8} }[/math]

Sí puede hacer el pastel.

3. Calcule[math]\displaystyle{ 1-(\frac{1}{2}+\frac{3}{50})=\frac{11}{25} }[/math] fracción de ovejas muertas.

Respuestas de la fase de cierre

Ejercicios del tema

Conocimiento y recuerdo

1. Identifica y examina las situaciones En esta parte se refuerza la habilidad de poder recordar determinada palabra o concepto, operación y luego emplearlo.

Calcule altura. [math]\displaystyle{ \frac{1}{2}\div\frac{1}{4}=2m; }[/math] altura=[math]\displaystyle{ \frac{1}{2}\div4\frac{1}{8}m; }[/math] área=[math]\displaystyle{ \frac{16}{5}*\frac{2}{3}=\frac{32}{14}m^2 }[/math]

Multiplique. [math]\displaystyle{ (\frac{2}{3})*(\frac{4}{5})=\frac{8}{15} }[/math]planteado con zanahorias; no plantado. [math]\displaystyle{ 1-\frac{8}{15}=\frac{7}{15} }[/math]

Despeje Q. [math]\displaystyle{ \frac{2}{3}Q=3-\frac{12}{5}\top Q=\frac{3}{5}(\frac{3}{2})\top Q=\frac{9}{10} }[/math]

Comprensión: Organiza y relaciona la información

2. Refuerza lo que lee y, asocia un número, una variable y una operación. La selección de elementos significativos le permite dar respuesta a la situación problemática.

Respuestas:

Multiplique. [math]\displaystyle{ (\frac{3}{8})(40)=15; (\frac{3}{5})(25)=15; }[/math] son iguales

Calcule. [math]\displaystyle{ \frac{5}{4}+17(\frac{1}{5})=4 \frac{13}{20} }[/math] no es cierto

Calcule [math]\displaystyle{ 4 \div\frac{1}{5}- \frac{9}{2}=15 \frac{1}{2} }[/math] pasos Multiplique.

Julio [math]\displaystyle{ \frac{4}{9} (270)=120m^2; }[/math]

Ana [math]\displaystyle{ \frac{2}{3} (270)=180m^2; }[/math]

Resultados de evaluación

Respuestas de la fase de análisis

3. Ordene los datos y plantee estrategias

Identifique diferencias y similitudes importantes en el conocimiento.

4. Calcule: Chocolate [math]\displaystyle{ (3/8) (48)=18 }[/math]; fruta [math]\displaystyle{ (2/5)(30)=12 }[/math]; leche [math]\displaystyle{ 48-18-12=18 }[/math] Simplifique: [math]\displaystyle{ 18/48=3/8; 12/48=1/4; 18/48=3/8 }[/math]

Calcule invitados dividiendo entre 1/4 y cantidad de helado necesario multiplicando por 1/4: [math]\displaystyle{ 5, 1\frac{1}{4}; 6,1\frac{1}{2}; 3\frac{3}{4}; 5, 3\frac{3}{4} }[/math]

Plantee una ecuación y despeje la variable [math]\displaystyle{ x+\frac{1}{8}=5\frac{1}{2}\top x=5\frac{1}{2}-\frac{1}{8}\top x=5\frac{3}{8} }[/math] crecimiento en los semestres

Utilización. Plantea una estrategia utilizando la información para resolver los problemas.

Llegar a soluciones efectivas en este nivel indica que se ha logrado un estímulo que le permite actuar con dominio del conocimiento.

5. Plantee y resuelva la ecuación: [math]\displaystyle{ x-\frac{x}{5}-\frac{x}{2}=12\top x-5\frac{7x}{10}=12\Rightarrow\frac{3x}{10}=12 }[/math]

[math]\displaystyle{ x=12\frac{10}{3}=40 }[/math] jocotes se comieron

Plantee la ecuación y resuelva para x: [math]\displaystyle{ \frac{7}{10}(40)=28 }[/math] jocotes

[math]\displaystyle{ x+\frac{x}{3}+\frac{x}{4}=2x-17\Rightarrow-\frac{5x}{12}=-17 }[/math]

[math]\displaystyle{ x=(17)-(\frac{12}{5})\Rightarrow x =\frac{204}{5}=40\frac{4}{5} }[/math]

Área de la mayor vivienda.

Capacidad o destreza para hacer algo bien o con facilidad.

Lo que estimula o incita a hacer algo.