Serie Aprendo y enseño/Matemáticas/Estadística para organizar y comunicar la información/Tema 5. Probabilidad

Inicio

Indicadores de logro

1. Calcula la probabilidad de un evento sobre un espacio muestral.
2. Calcula la probabilidad utilizando una tabla de distribución simple de frecuencias.
3. Calcula permutaciones y combinaciones.

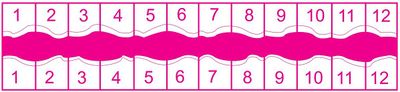
1. Elabore con cartulina un tablero como se muestra en la figura 1 y realice el siguiente juego.

• La franja central que se observa en la figura 1 representa un río con doce casillas numeradas del 1 al 12 a cada lado. Para este juego, se necesitan 24 fichas y dos dados.

Figura 1

Instrucciones

1. Participan dos jugadores; cada uno de los cuales dispone de 12 fichas.
2. Las fichas se deben colocar en cada una de las doce casillas (una ficha por casilla).
3. El primer jugador lanzará dos dados, sumará los puntos obtenidos en las caras superiores de los mismos y pasará la ficha a la casilla, del otro lado del río, con el número que ha obtenido al realizar la suma (puede armar dos dados como se observa en la figura 2).
4. A continuación, el segundo jugador lanzará los dados y repetirá el proceso.
5. Así se continúa hasta que alguno de los jugadores pase todas sus fichas al otro lado del río.

Figura 2

• ¿Es posible lograr el objetivo del juego? Explique.
• Tabule los datos según las veces que ocurra cada caso al tirar los dados.

Razonamiento matemático

El objetivo de pasar todas las fichas no se cumple para la primera posición, que nunca pasará el río. Realizarán el juego varias veces de manera que puedan descubrir que hay posiciones desde las que es más fácil pasar al otro lado y posiciones donde es imposible.

Desarrollo

Nuevos aprendizajes

Espacio muestral (S): es el conjunto de todos los resultados posibles de un experimento.

Evento (E): es todo subconjunto de un espacio muestral. Probabilidad: es qué tan posible pueda ocurrir un evento. La probabilidad de un evento se mide de la siguiente forma:

[math]\displaystyle{ P(E)=\frac{Las-veces-que-se-cuenta-el-evento}{Todos-los-elementos-del-espacio-muestral(s)} }[/math]

1. Analice.

En un experimento se lanzan dos dados al mismo tiempo y se suman los resultados. En la tabla 1 se muestran todas las posibles sumas que pueden resultar en cada lanzamiento.

Responda:

• ¿Cuántos eventos tiene el espacio muestral?
• ¿Cuál es la probabilidad de que la suma sea siete?
• ¿Cuál es la probabilidad de que la suma sea menor que siete?

Tabla 1

	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Al observar la tabla 1 y contar todos los eventos posibles, ese espacio muestral tiene 36 elementos.

• Para calcular la probabilidad de sumar siete, contamos cuántas veces se repite el número 7 en el espacio muestral:

[math]\displaystyle{ P(E)=\frac{Las-veces-que-se-cuenta-el-evento}{Todos-los-elementos-del-espacio-muestral(s)}=\frac{6}{36}=\frac{1}{6} }[/math]

Esta probabilidad puede expresarse como porcentaje al multiplicarla por 100; entonces, por cada 1/6*100=16.7% obtendremos una suma que dé 7.

• Para sumas menores de siete, contamos cuántas sumas son menores de ese número:

[math]\displaystyle{ P(E)=\frac{Las-veces-que-se-cuenta-el-evento}{Todos-los-elementos-del-espacio-muestral(s)}=\frac{15}{36}=\frac{5}{12} }[/math]

Como porcentaje, la probabilidad de que se obtenga una suma menor que 7 es: 5/12*100 = 41.7%.

Distribución de frecuencia

La distribución de frecuencia de un experimento permite establecer la probabilidad de que ocurra un evento que está en el espacio muestral.

Está definida por la frecuencia relativa y puede expresarse como porcentaje para tener una idea más clara de la posibilidad de que ocurra un resultado esperado.

2. Analice.

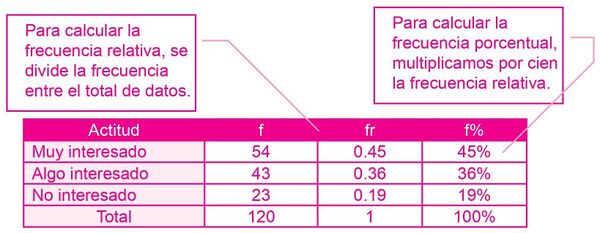
En una escuela se preguntó a 120 estudiantes acerca de si les gusta practicar un deporte. Los resultados se muestran en la tabla 2. Complete la tabla con la información de frecuencia relativa y porcentual.

Si encuentra a un estudiante de esa escuela:

a. ¿cuál es la probabilidad de que conteste “sí” al preguntarle si le interesa el deporte?

b. ¿cuál es la probabilidad de que le interese poco?

c. ¿cuál es la probabilidad de que no esté interesado?

Tabla 2

a. Según se observa en la tabla de distribución de frecuencia, se tiene una probabilidad de 45% de obtener un sí. b. La probabilidad de que el estudiante al que se le pregunte tenga un poco de interés es de 36%. c. Hay una probabilidad de 19% de que el estudiante no esté interesado.

Permutación y combinación

Permutación	Es un arreglo que se hace usando algunos o todos los elementos de un conjunto. Esta se denota: [math]\displaystyle{ P = n! }[/math]
Combinación	Es una selección de objetos en la que el orden no establece ninguna diferencia. Se denota: [math]\displaystyle{ c (n,r) =\frac{n!}{(n-r)!r!} }[/math]

• Enumere las distintas formas posibles para arreglar dos a dos las letras: a, b, c. P = 3! (se lee: tres factorial), esto es: 3! = 3 x 2 x 1 = 6 arreglos.
• Los arreglos son: ab, ac, ba, bc, ca, cb.
• Enumere las distintas combinaciones que podemos formar con las letras a, b, c. tomadas dos a dos. La combinación es : [math]\displaystyle{ c (3,2) =\frac{3!}{(3-2)!2!}=\frac{3 * 2 *1}{1*1*2}=\frac{6}{2}=3 }[/math]
• Responda cuáles son las combinaciones. Las combinaciones son: ab, ac, bc.

Cierre

Ejercicios del tema

Nivel: análisis

1. Resuelva.

La tabla 2 muestra los resultados del experimento de lanzar al aire tres monedas de veinticinco centavos al mismo tiempo, donde c= cara y e = escudo. Complete la tabla 2 en su cuaderno.

Tabla 2

Actitud	f	fr	f%
ccc	2
eee	3
cce	4
eec	5

Razonamiento matemático

Las frecuencias relativas son: 0.14, 0.21, 0.28 y 0.37. Las frecuencias porcentuales son: 14%, 21%, 28% y 37%.

a. 21%

b. 28%

c. 14% todas sean caras

d. Dos escudos y una cara

Sin importar el orden en el lanzamiento, responda:

a. ¿Cuál es la probabilidad de sacar todos como escudos?

b. ¿Qué porcentaje de probabilidad hay de sacar dos caras?

c. ¿Qué es menos probable que resulte en un lanzamiento?

d. ¿Cuál es el resultado que tiene un 37% de probabilidad?

2. Resuelva.

a. Si lanza una moneda al aire, ¿cuántas y cuáles opciones se tienen?

b. Si lanza un dado, ¿cuántas y cuáles opciones se tienen?

3. Explique cuál es la diferencia entre estas dos situaciones.

c. ¿Qué edad tendrán sus compañeros después de 10 años?

d. Si lanzamos dos monedas al aire, ¿qué posibilidad tenemos de que caigan: cara – cara?

4. Resuelva. En un experimento se lanzan un dado y una moneda a la vez:

e. ¿Cuál es el espacio muestral para este experimento?

f. ¿Cuál es la probabilidad de que salgan cara en la moneda y 3 en el dado?

Razonamiento matemático

a. Dos opciones, cara y escudo. b. Son seis opciones (1, 2, 3, 4, 5 y 6).

c. Es un valor que se puede determinar con exactitud.

d. En este caso, se tiene una probabilidad de 33.33%.

e. Espacio muestral S: S = [ (c,1), (c,2), (c,3), (c,4), (c,5), (c,6), (e,1), (e,2), (e,3), (e,4), (e,5), (e,6)]

f. La probabilidad de cara y 3 en el dado es de 8.33%.

5. Resuelva.

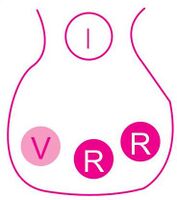
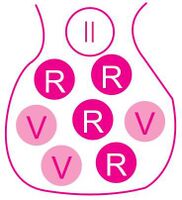
• La figura 3 muestra tres bolsas con pelotas rojas (R) y verdes (V).

• 
• 
• 

Figura 3

a. ¿De cuál de las tres bolsas es más probable sacar una bola roja?

b. ¿De cuál de las tres bolsas hay una probabilidad de 40% de sacar una bola verde?

c. Si se sacan dos bolas rojas juntas, ¿de qué bolsa es más probable hacerlo y cuál menos?

Razonamiento matemático

a. De la bolsa número I, debido a que la probabilidad es de 66.7%.

b. Del bolsa III.

c. La bolsa I es más probable con 66.7%, mientras que la menos probable es la bolsa II, con una probabilidad de 28.6%.

Resuelva las situaciones.

• Ignacio, Manuel, Rodrigo y Karla integran la junta directiva del salón de clases. Los puestos de presidente, vicepresidente, tesorero y secretario se pueden rotar cada cierto tiempo.

  a. Encuentre el número de arreglos o permutaciones posibles.

• Seis estudiantes del instituto forman un grupo de personas con talento para el canto. El instituto recibió una invitación para que tres de los seis estudiantes participen en un festival de arte.

  b. Encuentre el número de combinaciones posibles.

Razonamiento matemático

a. Las permutaciones posibles son P= 4!= 24.

b. Las combinaciones posibles para los estudiantes son:[math]\displaystyle{ c (6,3) =\frac{6!}{(6-3)!3!}=20 }[/math]