Serie Aprendo y enseño/Matemáticas/Relaciones y formas/Tema 3. Polígonos

Inicio

Indicadores de logro

1. Nombra e ilustra polígonos regulares e irregulares.
2. Resuelve problemas asociados a los ángulos internos de un polígono.
3. Utiliza información de los polígonos regulares para determinar perímetros y áreas.

Todas las actividades de este tema son para que usted realice. Si tiene oportunidad reúnase con otros docentes y compartan. Se recomienda aplicarlas con sus estudiantes del ciclo básico.

1. Lea y resuelva.

Las formas de la Figura 1 se llaman pentóminos, porque son 12 formas y cada una contiene cinco cuadros.

• Trace las formas de la figura 1 en una hoja milimetrada (1 cm) o cuadricula y recorte los pentóminos.
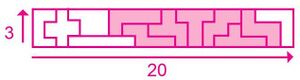
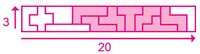
• Forme la figura 2, de tres cuadros de alto y 20 cuadros de largo, con los 12 pentóminos que recorte, encuentre el perímetro de la figura.
• Utilice los 12 pentóminos para forma una letra “L”, y encuentre el perímetro.
• Forme dos figuras más y calcule el perímetro, comparta sus hallazgos.

Figura 1

Figura 2

2. Lea, resuelva y exponga los resultados.

Cuando se cubre una superficie con un patrón de formas planas de manera que no se superponen ni hay espacios vacíos se dice que es una teselación.

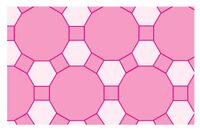
En la figura 3 muestra una teselación 4*8*8, llamada así, porque cada vértice es la unión de un cuadrado (4 lados) y dos octágonos (8 lados).

Figura 2

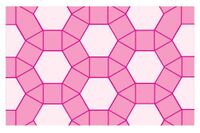
Marcos es alcalde de su municipio. El salón comunal necesita cambio de piso. Marcos se ha decidió por dos modelos de piso (figura 4), pero le surge una duda: ¿Cómo se forman tan maravillosas figuras?

• Escriba un mensaje a Marcos explicándole cómo se forman y el número para cada diseño.

• 
• 

Figura 4

Desarrollo

Nuevos aprendizajes

Un polígono es una figura plana formada por tres o más segmentos que se intersecan solo en los puntos extremos de manera que solo dos segmentos se tocan en cada punto extremo. Los polígonos reciben un nombre de acuerdo con el número de lados. En un polígono regular, todos los lados y ángulos miden lo mismo, cuando un polígono no es regular se llama irregular.

• Observe los polinomios de la figura 5.
  Clasifíquelos como regular o irregular según el número de lados. Explique sus hallazgos.

• 
• 
• 
• 

Figura 5

Cuadrilátero

Un cuadrilátero es un polígono con cuatro lados. La suma de las medidas de los ángulos de un cuadrilátero es igual a 360°.

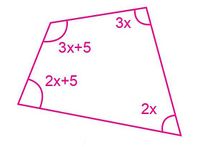
• Calcule x y sustituya para hallar los ángulos del cuadrilátero en la figura 6:
  2x + (2x +5) + (3x + 5) + 3x = 260; 10x + 10 = 360; x =35°

• Calcule el valor numérico de los ángulos del cuadrilátero si están representados por: x; (x + 6); (2x-2); (x +1)

Figura 6

Área de polígono

En un polígono regular sus lados son congruentes. Un polígono se puede descomponer en tantos triángulos isósceles como lados tenga. La altura de cada triángulo isósceles la consideramos como el segmento de recta perpendicular, trazado desde el punto O al lado del polígono y recibe el nombre de apotema. Entonces la región plana limitada por un polígono regular de n lados, es la unión de la n regiones triangulares en que se puede descomponer, entonces eso nos permite calcular el área de un polígono de la siguiente manera:

[math]\displaystyle{ Área_{polígono}= Área_{triángulo}*n_{triángulos}; }[/math] otra forma para hallar el área del polígono será:

[math]\displaystyle{ Área_{polígono}=\frac{Perimetro_{polígono}=*apotema}{2}=A=\frac {P * a}{2} }[/math]

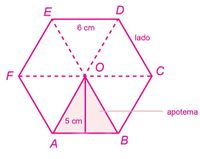
• Calcule el área del hexágono de la figura 6, de la siguiente manera:

[math]\displaystyle{ Área_{hexágono}\frac {6 * 6 * 5}{2}=\frac {180}{2}=90cm^2; }[/math]

• Calcule si ahora el lado del hexágono mide 10 cm y la apotema mide de 8 cm. Compare su resultado.

Cierre

Ejercicios del tema

Puede consultar las respuestas en la sección resultados a los ejercicios del tema

Nivel: Conocimiento y recuerdo

1. Identifique y examine las situaciones. Misael recortó los polígonos que se muestran en la figura 8, pero tiene dudas sobre los polígonos que observa.

• Identifique los polígonos y explique las diferencias y las similitudes entre ellos.

• 
• 
• 
• 
• 
• 
• 
• 

2. Plantee una estrategia para ayudar en la tarea y compártala.

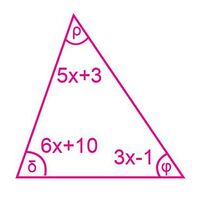
Jocabed tiene como tarea calcular los ángulos internos de los polígonos que se muestran en la figura 9.

• Encuentre x para cada polígono de la figura 9.
  Luego sustituya para calcular los ángulos de cada uno.

• 
• 

Figura 9

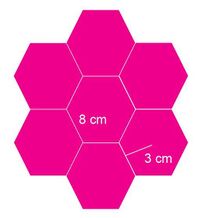
3. Calcule cuánto material necesita para hacerlas.
Explique su estrategia.

Noé tiene a su cargo hacer la figura 10, para la exposición matemática de mañana. Cuánto material necesita comprar, si él sabe que en la clase de matemáticas hay 15 estudiantes.

Figura 10

Nivel: Comprensión

4. Lea la información, organice y relacione.

La suma de los ángulos internos de un polígono convexo (todos los ángulos interiores son menores de 180°) de n lados es 180 (n -2). El número de triángulos formados dentro de polígono es (n -2).

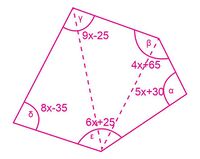
Encuentre la suma de los ángulos internos para el polígono de la figura 11.

• Calcule el valor de cada ángulo de la figura 11.
• Encuentre el valor de x. Explique sus hallazgos.

Figura 11

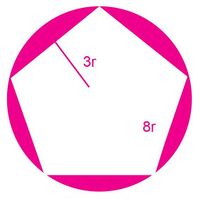
5. Plantee una estrategia para calcular el área utilizada para parqueo.

En la figura 12 se muestra el diseño de un centro comercial, donde el espacio para parqueo es la parte sombreada, el área del terreno circular es de 83r2.

• Encuentre la expresión que representa es área del parqueo.
• Calcule el área de parqueo si r = 2 metros.

Figura 12

Nivel: Análisis

6. Ordene los datos y plantee estrategias.

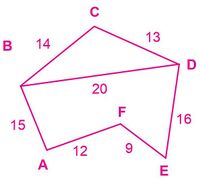
Don Rosalio necesita circular su terreno con alambre espigado con lo muestra la figura 13. Cada metro de alambre espigado tiene un valor de Q.4.50 y tiene Q.1700.00 para invertir, pero duda que sea suficiente.

• Observe la medida de los lados del terreno (en metros).
• Encuentre la cantidad de alambre que necesita Don Rosalio para circular cuatro veces el terreno.
• Calcule si es suficiente el presupuesto y para cuánto le alcanza.

Figura 13

7. Encuentre la expresión que representa el área total de un balón.

Francisco se dedica a fabricar balones de fútbol, sabe que necesita 12 pentágonos y 20 hexágonos para cada balón.

• Calcule cuánto cuero debe utilizar para fabricar una docena de balones, si el lado de los polígonos mide 4 cm y la apotema es de 2.5 cm.
• Ayude a Francisco a saber la ganancia que obtiene a vender los balones, si obtuvo Q.2,500.00, y el costo de producción es de Q.75.00 cada uno.

Figura 14

Nivel: Utilización

8. Plantee una estrategia utilizando la información para resolver los problemas.

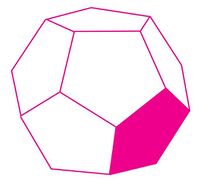
César se dedica en su tiempo libre a fabricar estructuras para bocinas, le han pedido que construya una como la figura 15, que tiene forma de dodecaedro regular (12 caras).

• Calcule cuánta madera debe comprar si cada cara tiene un lado que mide 25 cm y la apotema es de 10 cm.
• Recomiende cuánto puede cobrar por la bocina, si una plancha de madera que mide 100 cm x 50 cm cuesta Q.125.00.
• Explique su recomendación.

Figura 15

9. Plantee una estrategia para ayudar a Susan.

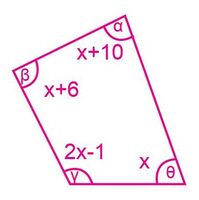
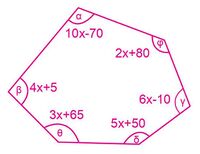
Florentino ha dibujado la piscina que quiere hacer en su patio como la figura 16, le pide a Susan su hija que la construya. Ella necesita determinar que ángulos debe darle a cada vértice para dar forma a la piscina.

• Encuentre el valor de x según su estrategia.
• Calcule los ángulos internos que necesita Susan.

Figura 16

Respuestas a los ejercicios del tema

Compruebe sus resultados a los ejercicios del tema con esta tabla.

Inicio

Es importante que elabore el material utilizando hojas de papel milimetrado o de papel cuadriculado.

Para la actividad 1, el perímetro se calcula contando de forma lineal los cuadritos de todo el contorno. Cuando realice esta actividad con estudiantes, revise que formen figuras según su creatividad.

En la actividad 2, el número de la figura 4, se encuentra al dibujar un punto sobre el vértice de un cuadrado y verificar en contra de las agujas del reloj: 4, 6, 12.

Para el número de la figura 5, dibuje un punto sobre el vértice de un cuadrado y verifique en contra de las agujas del reloj: 3, 4, 6, 4.

Cierre

Respuestas del nivel de conocimiento y recuerdo

En esta parte se refuerza la habilidad de poder recordar determinada palabra o concepto, operación y luego emplearlo.

1. Identifique que la primera fila de polígonos es regular y la segunda fila es irregular. En orden de derecha a izquierda hay un triángulo, cuadrilátero, pentágono y hexágono.

2. Para el cuadrilátero, sume los ángulos para que sean igual a [math]\displaystyle{ 360°. α=79°;β=75°; g=137°; q=69°. }[/math]

Para el triángulo se suman los ángulos igual a [math]\displaystyle{ 360° r=63°; d=82°; f=35°. }[/math]

3. Calcule el área del hexágono y multiplique por [math]\displaystyle{ (8*6*3)÷2*6=432 cm^2. }[/math]

Respuestas del nivel de comprensión

Organiza y relaciona la información.

Refuerza lo que lee y asocia un número, una variable y una operación.

La selección de elementos significativos le permite dar respuesta a la situación problemática.

4. Sume los ángulos internos e iguálelos a [math]\displaystyle{ 540º c=15°; α=105°; β=125°; e=115°; d=85°; g=110°. }[/math]

5. Encuentre el área sombreada restando el área del círculo menos el área de hexágono. [math]\displaystyle{ 83r^2- (8r*5*3r) }[/math] [math]\displaystyle{ 2=23r^2; A=23(2)^2= 92m^2. }[/math]

Respuestas del nivel de análisis

Ordena los datos y plantea estrategias Identifica diferencias y similitudes importantes en el conocimiento.

6. Calcule el perímetro sumando lados y multiplicando por 4.
[math]\displaystyle{ 4(99)=396m^2. }[/math]

El presupuesto no es suficiente: [math]\displaystyle{ 396 m^2*Q.4.5=Q.1782.00 }[/math] Hace falta circular [math]\displaystyle{ 396- 377.7=18.2 m. }[/math]

7. Sume 12 pentágonos más 20 hexágonos.

Sustituya y multiplique por la docena:[math]\displaystyle{ A=90(4) }[/math] [math]\displaystyle{ (25)=180*12=1260cm2. }[/math]

La ganancia será:[math]\displaystyle{ 2500- 900=Q.1600.00. }[/math]

Respuestas del nivel de utilización

Plantea una estrategia utilizando la información para resolver los problemas.

Llegar a soluciones efectivas en este nivel indica que se ha logrado un estímulo que le permite actuar con dominio del conocimiento.

8. Calcule [math]\displaystyle{ A=(25*10*5) ÷2*12=7500cm^2. }[/math]

Calcule y recomiende:[math]\displaystyle{ (7500÷5000)*Q.125.00=Q.187.5, }[/math] tiene que cobrar más que esta cantidad.

9. Sume los ángulos internos e iguales a [math]\displaystyle{ 720° c=20°; α=130°; β=85°; q=125°; d=150°; g=110°; f=120°. }[/math]

Destrezas fonológica que consiste en juntar fonemas o sílabas para formar una palabra.

Capacidad o destreza para hacer algo bien o con facilidad.

Lo que estimula o incita a hacer algo.