Tema 4. Congruencia y semejanza

Inicio

Indicadores de logro

1. Identifica la diferencia entre congruencia y semejanza.
2. Aplica el primer teorema de Thales para resolver problemas relacionados con triángulos.

1. Lea y resuelva.

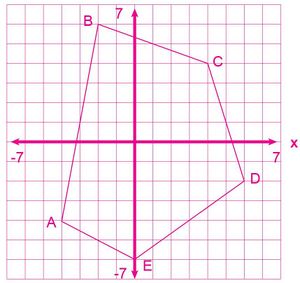
El polígono de la Figura 1 tiene sus vértices en las siguientes coordenadas cartesianas: A(- 4,- 4), B(2, 6), C(4, 4), D(6, - 2), E(0, - 6).

• Multiplique cada una de las coordenadas cartesianas por [math]\displaystyle{ 1/_2 }[/math] y obtenga coordenadas cartesianas para un nuevo polígono.
• Complete el cuadro 1 con los resultados obtenidos.
• Trace los dos polígonos en una hoja de papel milimetrado.

Figura 1

2. Responda a las siguientes preguntas.

• ¿Son congruentes las dos figuras geométricas?
• ¿Son semejantes las dos figuras geométricas?

Tabla 1

Coordenadas originales	A (- 4,- 4)	B (2, 6)	C(4, 4)	D(6, - 2)	E(0, - 6)
Coordenadas obtenidas	A´	B	C´	D´	E´

Las nuevas coordenadas cartesianas: A´ (- 2, -2), B´ (1, 3), C´ (2, 2), D´ (3, -1) y E´ (0,-3) forman una figura geométrica congruente con la original. Las figuras que tienen el mismo tamaño y la misma forma son congruentes. Una forma sencilla de comprobar la congruencia de las figuras es cortarlas y colocarlas una sobre la otra para comprobar que coinciden en sus partes correspondientes.

Las figuras que tienen la misma forma, pero no necesariamente el mismo tamaño, son figuras semejantes. Las figuras semejantes pueden considerarse como agrandamientos o reducciones de ellas mismas sin distorsiones. Para comprobar que los polígonos anteriores son semejantes, mida con una regla sus lados correspondientes y con un compás, el ángulo en cada uno de sus vértices. Si obtiene ángulos congruentes y lados proporcionales, las figuras son semejantes. Para comprobarlo deberá realizar estas mediciones.

Desarrollo

Nuevos conocimientos

Dos polígonos son semejantes si y solamente si los ángulos correspondientes son congruentes y los lados correspondientes son proporcionales.

1. Lea la siguiente situación.

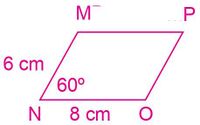
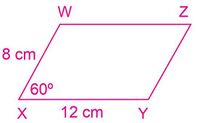
En la Figura 2, se muestran dos paralelogramos, ¿será que el paralelogramo MNOP es semejante al paralelogramo WXYZ?

• 
• 

Figura 2

Revise los siguientes enlaces para retroalimentar el conocimiento sobre congruencia y semejanza:

https://www.youtube.com/watch?v=aBPpHWrfovQ

https://www.youtube.com/watch?v=SBd-FcjJyHQ&feature=youtu.be

Para demostrar la semejanza de los paralelogramos, observe lo siguiente:

• El ángulo en el vértice N es [math]\displaystyle{ 60° }[/math] y el ángulo en el vértice X es [math]\displaystyle{ 60° }[/math].
• El ángulo en el vértice P es [math]\displaystyle{ 60° }[/math] y el ángulo en el vértice Z es [math]\displaystyle{ 60° }[/math].
• El ángulo en el vértice O es [math]\displaystyle{ 120° }[/math] y el ángulo en el vértice Y es [math]\displaystyle{ 120° }[/math].
• El ángulo en el vértice M es [math]\displaystyle{ 120° }[/math] y el ángulo en el vértice W es [math]\displaystyle{ 120° }[/math].

Conclusión: los ángulos correspondientes son congruentes.

Para evaluar si los lados son proporcionales, se realiza el siguiente procedimiento:

• [math]\displaystyle{ \frac{MN}{WX}=\frac{6}{8}=\frac{3}{4} }[/math], se relacionan los lados MN y WX con una fracción.
• [math]\displaystyle{ \frac{NO}{XY}=\frac{8}{12}=\frac{2}{3} }[/math], se relacionan los lados NO y XY con una fracción.

Los resultados evidencian que los paralelogramos no son proporcionales; por lo tanto, no son semejantes. La constante de proporcionalidad entre los lados de polígonos semejantes se llaman razón de semejanza. La Figura 4 muestra un paralelogramo QRST semejante al paralelogramo MNOP. En este caso, la razón de semejanza es: [math]\displaystyle{ 1/_3 }[/math].

Figura 3

En el siguiente enlace de geometría plana, repase la semejanza con GeoGebra. https://www.edu.xunta.gal/espazoAbalar/sites/espazoAbalar/files/datos/1491480036/contido/ud9_teorema_Thales_y_semejanza/23_razn_de_semejanza.html

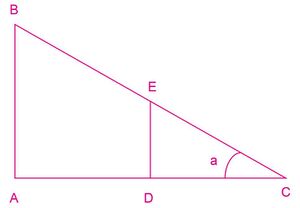
El primer teorema de Thales constituye una herramienta muy útil que, entre otras cosas, permite construir un triángulo semejante a otro, previamente conocido. El primer teorema de Tales enuncia que si, en un triángulo dado, se traza una recta paralela a cualquiera de sus lados, el nuevo triángulo que se obtiene será semejante al triángulo inicial. Vea la Figura 4.

La razón de semejanza para esta situación es:[math]\displaystyle{ \frac{AB}{DE}=\frac{AC}{CD} }[/math]

Figura 4

2. Analice la siguiente situación.

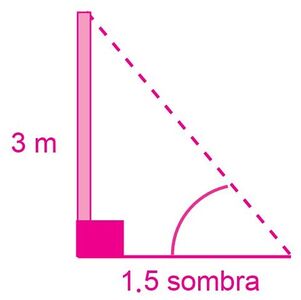
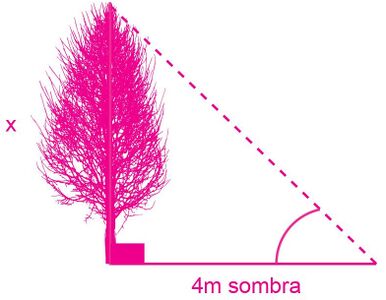
Un poste vertical de 3 metros proyecta una sombra de 1.5 metros. La Figura 5 muestra esta situación. ¿Qué altura tendrá un árbol que a la misma hora proyecta una sombra de 4 metros?

• 
• 

Figura 5

Si sitúa el triángulo que forma el poste dentro del triángulo que forma el árbol, comprobará que los triángulos son congruentes. Para esta situación evalúe que:

• La longitud del poste es proporcional a la longitud del árbol. Esto se escribe [math]\displaystyle{ 3/_x }[/math].
• La longitud de la sombra del poste es proporcional a la longitud de la sombra del árbol y se escribe así: [math]\displaystyle{ 1.5 /_4 }[/math].
• Se establece una relación de semejanza con la ecuación:[math]\displaystyle{ \frac{3}{x}=\frac{1.5}{4} }[/math], se obtiene que x = 8.
• Los productos cruzados permiten obtener una ecuación equivalente [math]\displaystyle{ (3) (4) = 1.5 (x) }[/math]; al resolver: [math]\displaystyle{ 12 = 1.5 (x) }[/math], se determina [math]\displaystyle{ x }[/math].
• En conclusión, la altura del árbol es de 8 metros.

Cierre

Ejercicios del tema

1. Lea y resuelva aplicando el teorema de Thales.

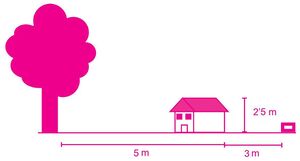
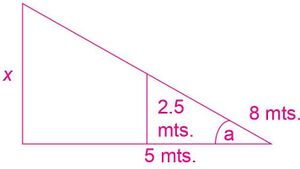
La altura de la casa de Alberto es de 2.5 metros, tal como se muestra en la Figura 6. Enfrente de la casa, hay una ceiba que se encuentra a 5 metros.

Además, la ceiba se encuentra a 8 metros de una jaula de gallinas ponedoras. ¿Cuál es la altura de la ceiba?

Figura 6

Razonamiento matemático

• Forme triángulos semejantes con la Figura 6, de tal forma que pueda aplicar el teorema de Thales.

• Observar que el gallinero es el vértice del triángulo que forma la ceiba y el triángulo de la casa.
• La relación de semejanza:[math]\displaystyle{ \frac{X.}{2.5}=\frac{8}{3} }[/math], resuelve la situación.
• Al resolver se obtiene que x = 6.6 metros o 20/3 metros de altura.

2. Aplique el teorema de Thales para determinar el valor de x.

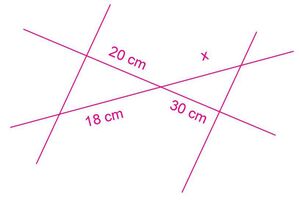
Dos rectas l1 y l2 son cortadas por dos rectas paralelas, tal como se muestra en la Figura 7.

Figura 7

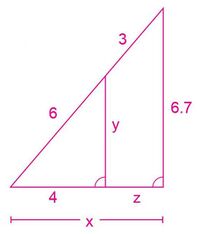
3. Determine el valor s x, y, z en la Figura 8. Utilice el Teorema de Thales.

Figura 8

Vea la solución a esta situación en el siguiente video:

Razonamiento matemático

El teorema de Thales se puede enunciar de la siguiente forma: si las rectas L1 y L2, se cortan por rectas paralelas, entonces los segmentos formados por las intersecciones son proporcionales.

Para este caso, la relación se escribe de la forma: [math]\displaystyle{ \frac{x}{18}=\frac{30}{20} }[/math]

Se escribe una ecuación al realizar productos cruzados:

[math]\displaystyle{ 20x = (18) (30) }[/math]

[math]\displaystyle{ 20x = 540, por lo tanto, x = 27. }[/math]

Conjunto de acciones (formas de actuar o de resolver tareas), con un orden, plan o pasos, para conseguir un determinado fin o meta. Se trata de saber hacer cosas, aplicar o actuar de manera ordenada para solucionar problemas, satisfacer propósitos o conseguir objetivos. Forman los contenidos procedimentales.