Tema 2. Teoría de números

Inicio

Indicadores de logro

1. Resuelve situaciones que involucren múltiplos y divisores con números naturales.
2. Emplea el mínimo común múltiplo mcm y el mínimo común divisor MCD para resolver situaciones cotidianas.

Todas las actividades de este tema son para que usted realice. Si tiene oportunidad reúnase con otros docentes y compartan. Se recomienda aplicarlas con sus estudiantes del ciclo básico.

1. Lea y resuelva.

El festival

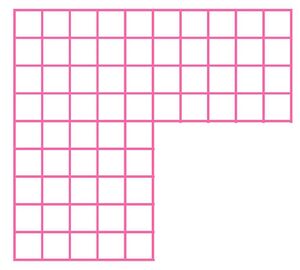
Para el festival del instituto se deben acomodar, en filas, 40 sillas para los invitados. La señora de limpieza dice que hay 8 maneras diferentes para acomodar las sillas de manera rectangular.

• ¿Cuáles son las 8 maneras diferentes de acomodar las 40 sillas?
• Responda en el cuaderno y comparta las soluciones con sus compañeros.
  Con la operación: 9x10-6x5, ¿también se puede calcular? Expliquen cómo se puede pensar de otras formas el arreglo de la figura 1

Figura 1

Más tarde, para la entrega de premios, se reacomodaron todas las sillas en 6 filas:

• ¿Cuántas sillas se colocaron en cada fila?
• ¿Cuántas formas de acomodar las sillas habría si fueran 80? ¿Y si fueran 100?

2. Lea, resuelva y exponga.

• En un supermercado tienen que cambiar las ruedas de sus 129 carros. Ya han puesto 342 ruedas. ¿Cuántas ruedas les quedan por poner, si cada carrito tiene 4 ruedas?
• En una bodega hay 87 litros de jugo de limón y 51 litros de agua. Para hacer limonada se mezclan el jugo de limón y el agua en una botella de 2 litros de capacidad. ¿Cuántas botellas se llenarán en total?

Desarrollo

Nuevos conocimientos

El producto de dos números enteros es un múltiplo de cada uno de ellos. Los múltiplos de un número se caracterizan por ser infinitos. Cuando se multiplica dos o más números para formar un producto, a cada uno se llama un factor o divisor del producto. Los factores o divisores de un número son finitos. Los múltiplos de un número se pueden encontrar multiplicando por 0,1, 2, 3, 4… etcétera (son infinitos). El 0 es múltiplo de todos los números naturales.

1. Encuentre 5 números que sean divisores de 270, si 18*15= 270. Escríbalos en el cuaderno.

Número primo y número compuesto

El número 7 tiene exactamente dos factores, 1 y 7. Cualquier número que tenga exactamente dos factores 1 y él mismo, se llama número primo. A cualquier número entero mayor que 1 y con más de dos factores o divisores se les llama número compuesto. El número 1 tiene un solo factor, por lo que no es primo ni compuesto.

2. Complete la tabla para encontrar el valor mínimo de n que dé un número compuesto en 6n+1.

n	0	1	2	3	4	5	6
6n+1	1

Potencia y exponente

Un producto en donde los divisores son idénticos se llama potencia de ese factor. Los exponentes se usan para escribir potencias en forma corta. El exponente indica el número de veces que la base se toma como factor. Para mostrar los factores de un número que se escribió usando exponentes, se escribe el número en forma desarrollada, también conocida como forma factorizada.

• Si 16=2*2*2*2= 24, ¿De cuántas formas diferentes puede escribir 256 y 81 en forma de una potencia? 24

[math]\displaystyle{ \begin{array}{c|c} 250 & 2 \\ 125 & 5 \\ 25 & 5 \\ 5 & 5 \\ 1 & \\ \end{array} }[/math]

[math]\displaystyle{ \begin{array}{c|c} 300 & 2 \\ 150 & 2 \\ 75 & 3 \\ 25 & 5 \\ 5 & 5\\ 1 & \\ \end{array} }[/math]

[math]\displaystyle{ 250 = 2 x 5^3 }[/math] [math]\displaystyle{ 300 = 2^2 x 3 x 5^2 }[/math] M.C.D.[math]\displaystyle{ = 2 X 5^2 = 50 }[/math]

[math]\displaystyle{ \begin{array}{c|c} 18 & 2 \\ 9 & 3 \\ 3 & 3 \\ 1 & \\ \end{array} }[/math]

[math]\displaystyle{ \begin{array}{c|c} 27 & 3 \\ 9 & 3 \\ 3 & 3 \\ 1 & \\ \end{array} }[/math]

[math]\displaystyle{ \begin{array}{c|c} 30 & 2\\ 15 & 3\\ 3 & 5 \\ 1 & \\ \end{array} }[/math]

[math]\displaystyle{ 18 = 3^2 x 2 }[/math] [math]\displaystyle{ 27 = 3^3 }[/math] [math]\displaystyle{ 30 = 2 x 3 x 5 }[/math] M.C.D. [math]\displaystyle{ = 3^3 x 5 x 2 = 27 x 5 x 2 = 270 }[/math]

Refuerce su aprendizaje consultando: https://www.matesfacil.com/ESO/numeros/problemas/problemas-resueltos-aplicacion-mcm-MCD-minimocomun-multiplo-Maximo-Comun-Divisior.html

De los números al algebra
Escriba el MCD (el menor exponente) y mcm (el mayor exponente) de las expresiones algebraicas.
	Expresiones	MCD	mcm
00)	[math]\displaystyle{ x^3; 2x; 6x^2 }[/math]	[math]\displaystyle{ x }[/math]	[math]\displaystyle{ 6^3 }[/math]
0)	[math]\displaystyle{ 15x^2y; 5xy^2; 30x^3y^3 }[/math]	[math]\displaystyle{ 5xy }[/math]	[math]\displaystyle{ 30x^3y^2 }[/math]
1)	[math]\displaystyle{ 3w^7x^2; 12w^2x^4; 6w^3x^3 }[/math]
2)	[math]\displaystyle{ 24r^9t^5; 8r^3t^6; 4r^6t^4 }[/math]
3)	[math]\displaystyle{ 12x^2yx^3; 18xy^2z; 24x^3yz^2 }[/math]

Refuerce su aprendizaje consultando: https://ejerciciosalgebra.wordpress.com/2013/06/12/minimocomun-multiplo-de-monomios/

Cierre

Ejercicios del tema

Nivel: Conocimiento y recuerdo. Identifica y examina las situaciones

1. Encuentre todos los factores y cinco múltiplos de: 12, 55 y 120.

• Plantee ideas en el cuaderno y compare los resultados.

2. Responda cuántos números primos menores de 100 existen.

• Elabore una tabla donde anote todos los números de 1 a 100.
• Como 2 es primo, rodee y tache los múltiplos de 2.
• El 3 es primo, rodee y tache los múltiplos de 3 que no estén tachados.
• Repita el procedimiento hasta llegar a 100 y cuente cuántos rodeó.

3. Escriba como producto o como potencia según lo indique la expresión:

a) 2*2*2*2*2*2*2*2*2*2*2

b) 5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5

c) 11*11*11*11*11*11*11*11*11*11*11*11

d) 2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2

e) n*n*n*n*n*n*n*n*n*n*n*n

f) a+a+a+a+a+a+a+a+a+a+a+a+a+a+a+a

• Trabaje en su cuaderno
• Elabore un cartel y explique los resultados.

Nivel: Comprensión. Organiza y relaciona la información

4. Complete el cuadro mágico que se muestra en la Figura 2, para ello se deben hallar los divisores de 216 (sin contar el 216). Elija otros 5 para completar el cuadrado mágico, sin repetir ninguno, de tal manera que el producto de tres factores en filas, columnas o diagonales sea siempre 216.

• Copie en el cuaderno el cuadro mágico de la Figura 2.
• Encuentre todos los factores de 216 y complete el cuadro mágico.
• Comparta los resultados con sus compañeros.

Figura 2

16	3	3
	6	36
12		0

5. Copie en su cuaderno la Tabla 1 y encuentre el MCD y mcm.

• Identifique y escriba la letra de la expresión según sus resultados. Explique.

Tabla 1

	Expresiones		MCD		mcm
a)	[math]\displaystyle{ x^3; 2x; 6x^2 }[/math]	()	[math]\displaystyle{ 6x^2y }[/math]	()	[math]\displaystyle{ 42x^4y^5 }[/math]
b)	[math]\displaystyle{ 15x^2y; 5xy^2; 30x^3y^3 }[/math]	()	[math]\displaystyle{ 7x^2y^2 }[/math]	()	[math]\displaystyle{ 36x^5y^3 }[/math]
c)	[math]\displaystyle{ 21x^4y^2; 42x^2y^5; 7x^2y^3 }[/math]	()	[math]\displaystyle{ 15x^3y^6 }[/math]	()	[math]\displaystyle{ 90x^10y^11 }[/math]
d)	[math]\displaystyle{ 6x^4y^2; 36x^5y^3; 18x^2y }[/math]	()	[math]\displaystyle{ x }[/math]	()	[math]\displaystyle{ 30x^3y^2 }[/math]
e)	[math]\displaystyle{ 90x^10y^8; 15x^6y^11; 45x^3y^6 }[/math]	()	[math]\displaystyle{ 5xy }[/math]	()	[math]\displaystyle{ 6x^3 }[/math]

Nivel: Análisis. Ordena los datos y plantea estrategias

6. Trabaje en el cuaderno y comparta sus resultados.

• Los números 180 y 345 son múltiplos de 15, utilice este dato para escribir dos factores de cada uno de estos números.
• Para averiguar si el número 191 es primo o compuesto, ha hecho las divisiones de ese número por 2, 3, 5, 7, 11, 13 y 17, respectivamente. En ningún caso la división ha sido exacta. ¿Puede asegurar que el número 191 es primo?
• Compruebe también con los siguientes números: 541, 137, 1337.
• Un grupo de excursionistas está formado por 72 chicos y 66 chicas. Si forma grupos iguales de chicos y chicas, ¿cuántos alumnos formarán cada grupo?

Utilización. Plantea una estrategia utilizando la información para resolver los problemas

7. Resuelva en el cuaderno, exponga la estrategia y los resultados obtenidos.

• El producto de tres números es 360.
• ¿Cuáles pueden ser estos tres números?
• ¿Puede escribir todas las soluciones del problema?
• Los alumnos de primero y segundo han ido de excursión, en total 123 alumnos. El número de alumnos de primero es igual a 3, más del cuádruplo de alumnos de segundo.
  ¿Determine cuántos alumnos de cada curso han ido?
• Carlos sugirió un plan a sus padres para su mesada. Él obtendría 1 centavo el primer día, 2 el segundo día, 4 el tercer día, 8 el cuarto día, y así sucesivamente. Si los padres de Carlos aprueban el plan, ¿determine cuánto obtendrá el quinceavo día? Para analizar este problema elabore una tabla para observar el comportamiento:

centavos	día	Patrón
1	1	[math]\displaystyle{ 2^0 }[/math]
2	2	[math]\displaystyle{ 2^1 }[/math]
4	3	[math]\displaystyle{ 2^2 }[/math]
8	4	[math]\displaystyle{ 2^3 }[/math]
1024= Q.10.24	10	[math]\displaystyle{ 2^{10} }[/math]

8. Calcule lo siguiente.

• Una gacela joven realiza saltos de 6 metros, mientras que una adulta da saltos de 8 metros.
  Si una gacela joven comienza a dar saltos y desde la primera huella ponga a una adulta para que la siga.
• Calcule, ¿cuántos metros recorrerá la gacela adulta hasta que vuelva a pisar una huella de la joven?
• Determine, ¿cuántos saltos dio la gacela adulta hasta la segunda coincidencia y cuántos saltos dio la gacela joven?

Resultados a los ejercicios del tema

Compruebe sus resultados a los ejercicios del tema con esta tabla.

Respuestas de la fase de inicio

1. Respuesta: factores de 40 los posibles valores: 10x4;5x8;20x5;40x1; 4x10;8x5;5x20;1x40

La suma las áreas de los rectángulos en forma de producto es: 10x4+4x5=40.

Respuesta: el rectángulo total menos el rectángulo vacío (sin sillas): 9x10-6x5=60

Respuesta: 10 silla en cada una, ya que 6x10=60

Las cantidades: 80:40x2;20x4;10x8;5x16; 80x1 100: 50x2; 25x4; 5x20; 100x1

2. Respuesta: 129 carros con 4 ruedas y se han puesto 342 ruedas; entonces: 129x4-342=174 ruedas faltan por instalar.

Como es una mezcla y se quieren llenar botellas de 2 litros, entonces 87+51=138÷2=69 litros de limonada 6x6 = 36+1 = 37

Respuestas de la fase de cierre

Ejercicios del tema

Conocimiento y recuerdo: Identifica y examina las situaciones

En esta parte se refuerza la habilidad de poder recordar determinada palabra o concepto, operación y luego emplearlo.

Respuestas:

1. En el caso del 12 los factores serán: 6x2; 4x3; 12x1 y los múltiplos podrían ser: 12x1=12; 12x2=24; 12 x 3=36;12x4=48; 12x5=60.

En el caso del 55 los factores serán: 55x1;55x11, los múltiplos pueden ser: 55x1=55; 55x2=110; 55x3=165; 55x4=220; 55x5=275

2. Respuesta: 25 números primos menores de 100. 3.

a)211

b)5x16

c)1112

d)2x16

e)n12

f)16a

Comprensión: Organiza y relaciona la información Refuerza lo que lee y, asocia un número y una operación. La selección de elementos significativos le permite dar respuesta a la situación problemática

Respuestas:

4. Factorización del número 216= {2,4,6,8,9,12,18,27,36,54,108}; el cuadro se completa con el cuadro mágico con: primera columna 18, 1, 12; segunda columna 4, 6, 9; tercera columna 3, 36, 2.

5. Las soluciones por fila son: c,d; d,c; e,e; a,b; b,a.

Respuestas de la fase análisis

Ordena los datos y plantea estrategias

Identifica diferencias y similitudes importantes en el conocimiento.

6. Respuestas:

Para hallar los factores dividimos y el cociente resultante será el otro factor de tal manera que: 180÷15=12 entonces 12x15=180; 345÷15=23 entonces 23x15=345.

Se comprueba que cada uno de los números son primos, haciendo divisiones

Encuentre del MCD de 72 y 66, es cual es 6, luego 72÷6=12 y 66=11.

Al interpretar serán 6 grupos de cada género y los grupos de chicos serán de 12 y los grupos de chicas serán 11.

Utilización. Plantea una estrategia utilizando la información para resolver los problemas

Llegar a soluciones efectivas en este nivel indica que se ha logrado un estímulo que le permite actuar con dominio del conocimiento.

Respuestas:

7. Factorización de 360=23, 32, 5. Estas son algunas combinaciones posibles: 5x6x12; 4x6x15; 5x9x8; 3x15x8.

Plantear la ecuación: primero = 4x+3; segundo = x; la ecuación será (4x+3)+x=123, al despejar x=24 alumnos de segundo y los de primero serán 99.

8. Ambas tocarán la misma marca en 24 metros, b) la gacela adulta dará 6 saltos para el segunda marca porque 6x8=48 (segunda marca), c) la gacela joven dará 8 saltos porque 8x6= 48

Término utilizado, a menudo, como un saber hacer. Se suele aceptar que, por orden creciente, en primer lugar estaría la habilidad, en segundo lugar la capacidad, y la competencia se situaría a un nivel superior e integrador. Capacidad es, en principio, la aptitud para hacer algo. Todo un conjunto de verbos en infinitivo expresan capacidades (analizar, comparar, clasificar, etc.), que se manifiestan a través de determinados contenidos (analizar algo, comparar cosas, clasificar objetos, etc.). Por eso son, en gran medida, transversales, susceptibles de ser empleadas con distintos contenidos. Una competencia moviliza diferentes capacidades y diferentes contenidos en una situación. La competencia es una capacidad compleja, distinta de un saber rutinario o de mera aplicación.

Conjunto de acciones (formas de actuar o de resolver tareas), con un orden, plan o pasos, para conseguir un determinado fin o meta. Se trata de saber hacer cosas, aplicar o actuar de manera ordenada para solucionar problemas, satisfacer propósitos o conseguir objetivos. Forman los contenidos procedimentales.

Capacidad o destreza para hacer algo bien o con facilidad.

El género es un conjunto de valores, creencias e ideas sobre los comportamientos y actividades que en una determinada cultura son adecuados para las mujeres y los que son adecuados para los hombres, es decir, su identificación con la femineidad y con la masculinidad.

Lo que estimula o incita a hacer algo.